Truss
In the truss diagram below, calculate the reaction at point A.
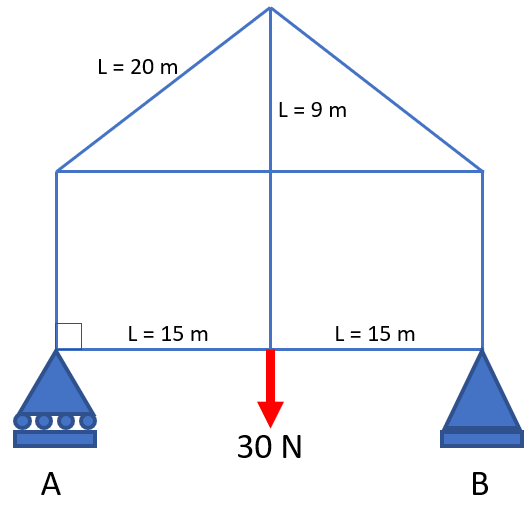
Expand Hint
The problem is asking to solve for
$$A_y$$
in the free body diagram below:
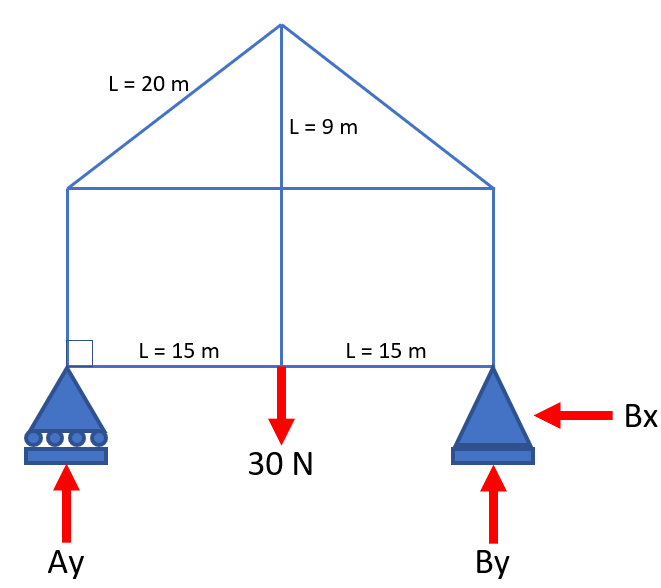
Hint 2
Due to point A being a roller support, there is only a vertical component force
$$A_y$$
. Point B is a fixed support, so there is both a vertical and horizontal component (
$$B_y$$
and
$$B_x$$
respectively). The problem statement is asking for the reaction at point A, so let's analyze the moments about point B.
The problem is asking to solve for
$$A_y$$
in the free body diagram below:
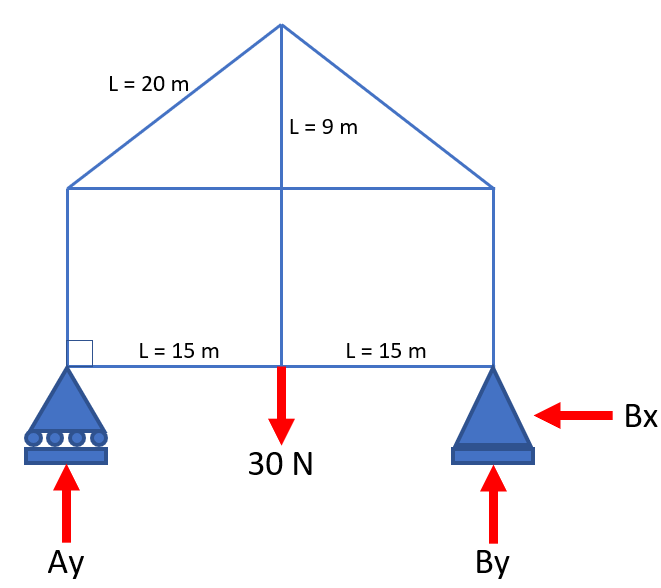
Due to point A being a roller support, there is only a vertical component force
$$A_y$$
. Point B is a fixed support, so there is both a vertical and horizontal component (
$$B_y$$
and
$$B_x$$
respectively). The problem statement is asking for the reaction at point A, so let's analyze the moments about point B.
Assuming clockwise is positive, the sum of moment about B are zero:
$$$\sum M_B=0$$$
Remember, Moment = Force Applied at Point x Distance to Point
$$$\sum M_B=0=30N(15m)-A_y(15m+15m)$$$
$$$A_y(30m)=450N\cdot m$$$
$$$A_y=\frac{450N\cdot m}{30m}=15\:N$$$
15 N
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked