Velocity-Time Graph
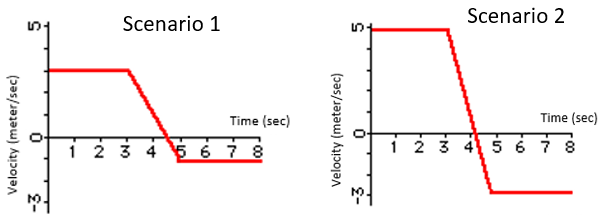
Consider the two velocity vs time graphs below.
- Which scenario has the greater velocity change?
- Which scenario has the greater acceleration?
- Which scenario has the greater momentum change?
- Which scenario has the greater impulse?
Hint
$$$Force=mass\cdot acceleration=mass\cdot \frac{\Delta velocity}{\Delta time}$$$
Hint 2
$$$Impulse=Change\:in\:momentum$$$
Looking at the two graphs, both scenarios are experiencing a velocity change from the three to five second mark (x-axis). Therefore, if we evaluate the change in the y-axis direction (velocity) for this time range, we can determine the greater velocity change.
$$$v_1=3-(-1)=4\:m/s$$$
$$$v_2=5-(-3)=8\:m/s$$$
(1.) Scenario 2 has the larger velocity change.
Acceleration is defined as:
$$$acceleration=\frac{\Delta velocity}{\Delta time}$$$
$$$a_1=\frac{4}{2}=2\:m/s^2$$$
$$$a_2=\frac{8}{2}=4\:m/s^2$$$
(2.) Scenario 2 has the larger acceleration.
Impulse is defined as
$$force\cdot time$$
, while momentum is defined as
$$mass\cdot velocity$$
, and the change in momentum is
$$mass\cdot \Delta velocity$$
. Therefore, if we multiple both sides of Newton' second law (
$$F=ma$$
) equation by
$$\Delta t$$
:
$$$Force \cdot \Delta time=mass\cdot \Delta velocity$$$
$$$Impulse=Change\:in\:momentum$$$
(3.) Scenario 2 has the larger momentum change. Since mass is constant, the velocity change will dictate the greater momentum change.
(4.) Scenario 2 has the larger impulse. Impulse is momentum change, and the momentum change is greatest in scenario 2.
(1.) Scenario 2 has the larger velocity change.
(2.) Scenario 2 has the larger acceleration.
(3.) Scenario 2 has the larger momentum change.
(4.) Scenario 2 has the larger impulse.