Construction Crane
Consider a construction crane in the below diagram is suspending a 40 kg payload. What is the tension in the diagonal cable that is supporting the load? Assume the crane arm is weightless.
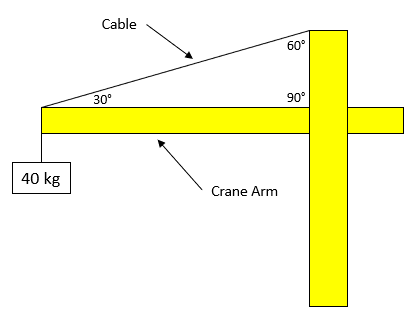
Expand Hint
The problem is asking to solve for the y-component of
$$F_{tension}$$
in the free body diagram below:
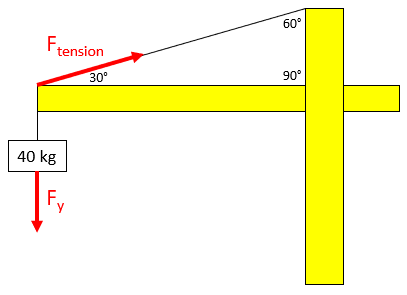
Hint 2
To find
$$F_y$$
, we can multiply the mass by gravity (Newton's 2nd law):
$$$F_y=mass\times acceleration$$$
The problem is asking to solve for the y-component of
$$F_{tension}$$
in the free body diagram below:
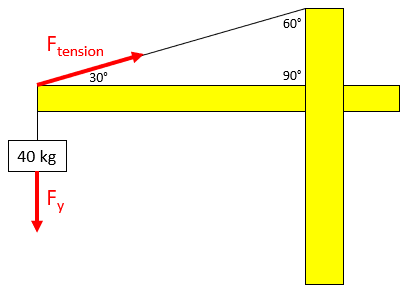
To find
$$F_y$$
, we can multiply the mass by gravity (Newton's 2nd law):
$$$F_y=mass\times acceleration=40kg\times 9.8m/s^2=392\:N$$$
Because there is only one upward pulling cable in the vertical direction, it will counteract the entire downward force. Thus:
$$$F_y=F_{tension}\cdot sin(30)=392N$$$
$$$F_{tension}=\frac{392N}{sin(30)}=\frac{392N}{0.5}=784\:N$$$
Despite the payload only causing a 392 N downward force, the cable has to work twice as hard to suspend the object due to its diagonal positioning.
784 N
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked