Acceleration Graph
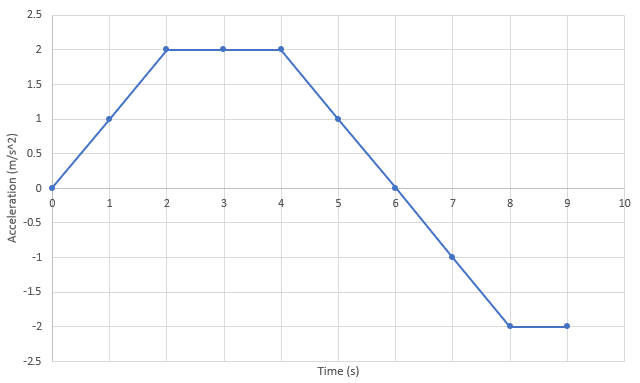
The below graph plots the acceleration of a motorcycle racing on a track. If the bike started from rest, what is its speed at the 7 seconds mark?
Expand Hint
Speed is the velocity integral with respect to time:
$$$Speed=initial\:speed+\int_{0}^{t}a\:dt$$$
Hint 2
By solving an integral, you are calculating the area under the curve. Thus, we can break down the graph by segments:
- 0-2 is a triangle
- 2-4 is a rectangle
- 4-6 is a triangle
- 6-7 is a triangle (in the negative direction)
Speed is the velocity integral with respect to time:
$$$Speed=initial\:speed+\int_{0}^{t}a\:dt$$$
$$$=0+\int_{0}^{2}a\:dt+\int_{2}^{4}a\:dt+\int_{4}^{6}a\:dt-\int_{6}^{7}a\:dt$$$
By solving an integral, you are calculating the area under the curve. Thus, we can break down the graph by segments:
- 0-2 is a triangle: $$\frac{1}{2}bh=\frac{1}{2}(2)(2)=2$$
- 2-4 is a rectangle: $$bh=2(2)=4$$
- 4-6 is a triangle: $$\frac{1}{2}bh=\frac{1}{2}(2)(2)=2$$
- 6-7 is a triangle (in the negative direction): $$-\frac{1}{2}bh=-\frac{1}{2}(1)(1)=-\frac{1}{2}$$
Combining all the segments together to find the speed at 7 seconds from initial launch:
$$$0+2+4+2-\frac{1}{2}=7.5\:m/s$$$
7.5 m/s
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked