Moving Boxes
In the diagram below, a moving truck is parked, ready to be unloaded. Two 4 kg boxes are arranged so that Box 2 rests on top of Box 1. The boxes are situated at the very back of the storage space, adjacent to the partially opened loading door, which only allows Box 1 to be pulled out. If the kinetic friction between the boxes is 0.3, and the kinetic friction between Box 1 and the floor is 0.1, what is Box 1's acceleration when the movers apply a 35 N force to pull it out?
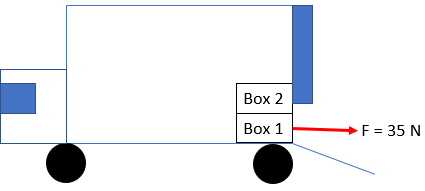
Expand Hint
The problem can be broken down at the two areas where friction is applicable: Box 2 on Box 1, and Box 1 on the bottom floor surface.
$$$F_{friction}=\mu_k(mass)(acceleration)$$$
Hint 2
Combining both friction sections, we can evaluate the forces on Box 1:
$$$\sum Forces=mass \times acceleration$$$
The problem can be broken down at the two areas where friction is applicable. Let's analyze the upper frictional force due to Box 2 on Box 1:

$$$F_{friction}=\mu_k(mass)(acceleration)$$$
$$$F_{upper}=(0.3)(4kg)(9.8m/s^2)=11.76\:N$$$
Next, let's evaluate the lower frictional force on Box 1 due to the bottom floor surface:
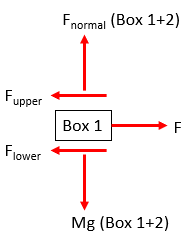
$$$F_{lower}=(0.1)(4kg+4kg)(9.8m/s^2)=7.84\:N$$$
Combining both friction sections, we can evaluate the forces on Box 1:
$$$\sum F=ma$$$
$$$F-F_{upper}-F_{lower}=ma$$$
$$$35N-11.76N-7.84N=(4kg)a$$$
Finally to solve for acceleration:
$$$a=\frac{15N}{4kg}=3.85\:m/s^2$$$
$$$3.85\:m/s^2$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked