Cart on a Ramp
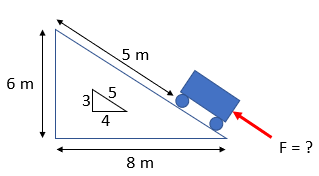
In the diagram below, a 4 kg cart is accelerated up a ramp from rest by an unknown force (F) for 5 m until it reaches the top with a speed of 10 m/s. Calculate the unknown force.
Expand Hint
Law of Conservation of Energy:
$$$KE_1+PE_1+W_{1\rightarrow 2}=KE_2+PE_2$$$
where
$$KE_1$$
is the initial kinetic energy,
$$PE_1$$
is the initial potential energy,
$$KE_2$$
is the final kinetic energy,
$$W_{1\rightarrow 2}$$
is the work inputted into the system, and
$$PE_2$$
is the final potential energy.
Hint 2
Kinetic Energy is:
$$KE=1/2mv^2$$
, where
$$m$$
is the mass and
$$v$$
is the velocity. Potential Energy is:
$$PE=mgh$$
, where
$$m$$
is the mass,
$$g$$
is the acceleration due to gravity, and
$$h$$
is the height.
Law of Conservation of Energy:
$$$KE_1+PE_1+W_{1\rightarrow 2}=KE_2+PE_2$$$
where
$$KE_1$$
is the initial kinetic energy,
$$PE_1$$
is the initial potential energy,
$$KE_2$$
is the final kinetic energy,
$$W_{1\rightarrow 2}$$
is the work inputted into the system, and
$$PE_2$$
is the final potential energy.
In our scenario, we evaluate the situation at rest (position 1), and right before the cart launches off the ramp (position 2). Since our cart starts at rest at the bottom of the ramp, both initial kinetic and potential energy are zero. However, our work (
$$W=Force\times distance$$
) is applicable. In position 2, there is both kinetic and potential energy due to the cart having a velocity and being farther along the ramp's top. Since
$$KE=1/2mv^2$$
and
$$PE=mgh$$
, our equation is:
$$$0+0+F\cdot x=\frac{1}{2}mv^2+mgh$$$
$$$F\cdot (5m)=\frac{1}{2}(4kg)(10m/s)^2+(4kg)(9.8m/s^2)(3m)$$$
Note that our ramp is a 3-4-5 triangle, so having moved 5 m along the ramp's top, our cart traveled 3 m vertically from its initial starting position. Inputting a 6 m height for
$$PE_2$$
would be incorrect.
$$$F=\frac{200N\cdot m+117.6N\cdot m}{5m}=63.52\:N$$$
63.52 N
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked