Plane Truss
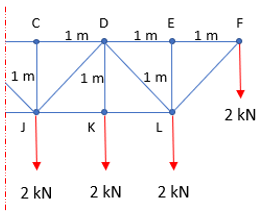
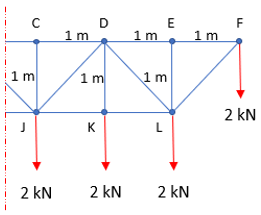
In the below figure, what is the force in Section BC?

Expand Hint
Because of the truss design, take an imaginary cut between section BC to simplify the figure. If we take the sum of moments about Point J, we can solve for the unknown force in Section BC.
Hint 2
If we take the sum of moments about Point J, we can solve for the unknown force in Section BC.
$$$\sum M_J=force\times distance =0$$$
Because of the truss design, take an imaginary cut between section BC to simplify the figure. If we take the sum of moments about Point J, we can solve for the unknown force in Section BC.
$$$\sum M_J=force\times distance =0$$$
$$$=M_C-M_K-M_L-M_F=0$$$
Because we are looking evaluating the sum of moments about Point J, the 2 kN on point J is zero. In addition, the moment from Point C is counteracting the other moments, so
$$M_C$$
is positive, unlike the others.
$$$(F_{BC})(1m)-(2kN)(1m)-(2kN)(1+1)m-(2kN)(1+1+1)m=0$$$
$$$(F_{BC})(1m)-2kN\cdot m-4kN\cdot m-6kN\cdot m=0$$$
$$$F_{BC}=\frac{12kN\cdot m}{1m}=12\:kN$$$
12 kN
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked