Torsion
In the below diagram, section OA is a solid titanium cylinder that is connected to section AB, which is a hollow steel pipe. What is the max shear stress in section AB?
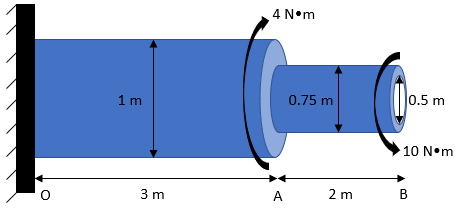
Expand Hint
$$$\tau =\frac{Tr}{J}$$$
where
$$\tau$$
is torsion,
$$T$$
is the torque at the section of interest,
$$r$$
is the radius to the point of interest, and
$$J$$
is the section's polar moment of inertia.
Hint 2
Polar moment of inertia of a hollow cylinder shaft:
$$$J_{hollow}=\frac{\pi (D_{outer}^{4}-D_{inner}^{4})}{32}$$$
where
$$D$$
is the diameter.
Torsional stress in circular solid or thick-walled (t<0.1r) shafts:
$$$\tau =\frac{Tr}{J}$$$
where
$$\tau$$
is torsion,
$$T$$
is the torque at the section of interest,
$$r$$
is the radius to the point of interest, and
$$J$$
is the section's polar moment of inertia.
Polar moment of inertia of a hollow cylinder shaft:
$$$J_{hollow}=\frac{\pi (D_{outer}^{4}-D_{inner}^{4})}{32}$$$
where
$$D$$
is the diameter.
$$$J=\frac{\pi ((0.75m)^{4}-(0.5m)^{4})}{32}=\frac{\pi(0.3164-0.0625)m^4}{32}=0.025\:m^4$$$
Thus,
$$$\tau=\frac{10N\cdot m(\frac{0.75}{2}m)}{0.025\:m^4}=150\frac{N}{m^2}=150\:Pa$$$
150 Pa
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Section: Torsion
058. Torsion on a Circular Rod
241. Torque Torsion
524. Solid Circular Rod
531. Circular Solid