Statically Indeterminate
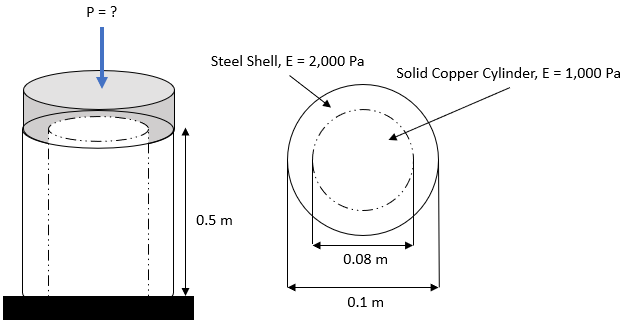
Consider a hollow steel shell encloses a solid copper cylinder on a test bench. Both are simultaneously subjected to a load, P, through a plate acting as a cap from the top. What load P is required to compress both the shell and solid cylinder by 0.01 m?
Expand Hint
This type of problem is referred to as statically indeterminate, because you can't determine the answer by only considering the statics. In all statically indeterminate problems, we use both the statics and the displacements together to determine the solution.
Hint 2
For uniaxial deformation:
$$$Deformation=\delta =\frac{PL}{AE}$$$
where
$$P$$
is loading,
$$L$$
is the length of member,
$$A$$
is the cross sectional area, and
$$E$$
is the modulus of elasticity
This type of problem is referred to as statically indeterminate, because you can't determine the answer by only considering the statics. In all statically indeterminate problems, we use both the statics and the displacements together to determine the solution. First, let's apply statics at the cap:
$$$\sum F=0\rightarrow P=P_{Steel}+P_{Copper}$$$
In this situation, compression in both cylinders are identical due to the fixed bottom test bench, and the cap. Thus, deformations are equal:
$$$\delta_{Steel}=\delta_{Copper}$$$
For uniaxial deformation:
$$$Deformation=\delta =\frac{PL}{AE}$$$
where
$$P$$
is loading,
$$L$$
is the length of member,
$$A$$
is the cross sectional area, and
$$E$$
is the modulus of elasticity. Solving for the force in the steel shell:
$$$P_{Steel}=\frac{AE}{L}\delta=\frac{[\frac{\pi }{4}(0.1m-0.08m)^2](2,000Pa)}{0.5m}(0.01m)$$$
$$$=\frac{\frac{\pi }{4}(0.0004m^2)(2,000N)}{0.5(m^2)}(0.01)=0.0126\:N$$$
Solving for the force in the copper cylinder:
$$$P_{Copper}=\frac{[\frac{\pi }{4}(0.08m)^2](1,000Pa)}{0.5m}(0.01m)=0.1\:N$$$
Finally, the total force:
$$$P=P_{Steel}+P_{Copper}=0.1N+0.0126N=0.113\:N$$$
0.113 N
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked