Water Gate
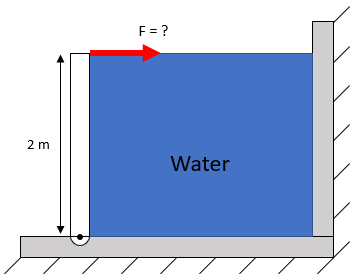
In the figure below, consider a 2 m high and 1 m wide rectangular gate is attached via a frictionless hinge at its base, and is holding back a tank of water. If water has a density of 1,000 kg/m^3, what force is required to keep the gate closed?
Expand Hint
$$$Pressure=\rho gh=\frac{Force}{Area}$$$
Hint 2
Since atmospheric pressure acts on both the non wet side of the gate, and the body of water's surface, the resultant force acting on the gate is:
$$$F_{R}=(\rho gh)sin\theta(A)$$$
where
$$\rho$$
is the density,
$$g$$
is gravity,
$$h$$
is height, and
$$A$$
is area.
Remember:
$$$Pressure=\rho gh=\frac{Force}{Area}$$$
$$$Force=\rho gh(Area)$$$
Since atmospheric pressure acts on both the non wet side of the gate, and the body of water's surface, the resultant force acting on the gate is:
$$$F_{R}=(\rho gh)sin\theta(A)$$$
where
$$\rho$$
is the density,
$$g$$
is gravity,
$$h$$
is height, and
$$A$$
is area. In our situation, the mean pressure of the fluid acting on the gate is evaluated at the mean height, and the gate is completely vertical, so
$$\theta = 90$$
degrees. Thus,
$$$F_R=(1,000\frac{kg}{m^3})(9.8\frac{m}{s^2})(\frac{2m}{2})(sin90^{\circ})(2m\times 1m)$$$
$$$F_R=(1,000\frac{kg}{m^3})(9.8\frac{m}{s^2})(1)(1m)(2m^2)=19,000\frac{kg\cdot m}{s^2}=19,000\:N$$$
Next, let's determine where the center of pressure is, which is where the resultant force is applied:
$$$y_{CP}=y_C+\frac{I_{xC}}{y_CA}$$$
where
$$y_C$$
is the gate's centroid,
$$I_{xC}$$
is the moment of inertia about the centroidal x-axis for a rectangle, and
$$A$$
is the area.
$$$I_{xC}=\frac{(base)(height)^3}{12}=\frac{(1m)(2m)^3}{12}=0.67m^4$$$
Thus,
$$$y_{CP}=(\frac{2m}{2})+\frac{0.67m^4}{(\frac{2m}{2})(2m\times1m)}=1m+\frac{0.67m^4}{2m^3}=1.33\:m$$$
The resultant force is 1.33 m from the water's surface, or 0.67 m above the hinge. Performing a moment balance about the hinge:
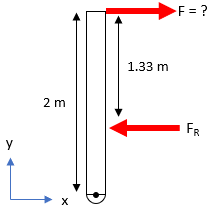
$$$\sum M_{hinge}=0=force\times distance$$$
$$$F_R(0.67m)-F(2m)=0$$$
$$$F=\frac{(19,000N)(0.67m)}{2m}=6,365\:N$$$
6,365 N
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Characteristics of a Static Liquid