Steam Tables
Saturated water at 115°C flows into a throttling valve, and exits the valve at 0.10135 MPa. At exit, what is the quality of the water?
Expand Hint
Quality, x, (for two-phase liquid-vapor systems at saturation) is defined as
$$$h=xh_g+(1-x)h_f\:or\:h=h_f+xh_{fg}$$$
where
$$h_{fg}$$
is the enthalpy change for phase transitions (evaporation),
$$h_f$$
is the enthalpy of saturated liquid,
$$h_g$$
is the enthalpy for saturated vapor, and
$$h$$
is specific enthalpy.
Hint 2

Quality, x, (for two-phase liquid-vapor systems at saturation) is defined as
$$$h=xh_g+(1-x)h_f\:or\:h=h_f+xh_{fg}$$$
where
$$h_{fg}$$
is the enthalpy change for phase transitions (evaporation),
$$h_f$$
is the enthalpy of saturated liquid,
$$h_g$$
is the enthalpy for saturated vapor, and
$$h$$
is specific enthalpy.
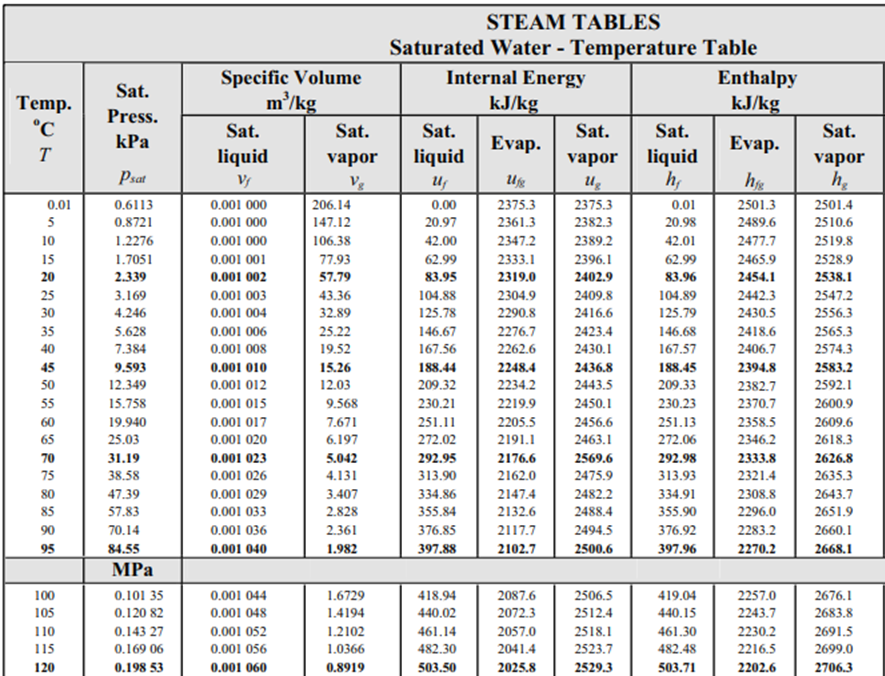
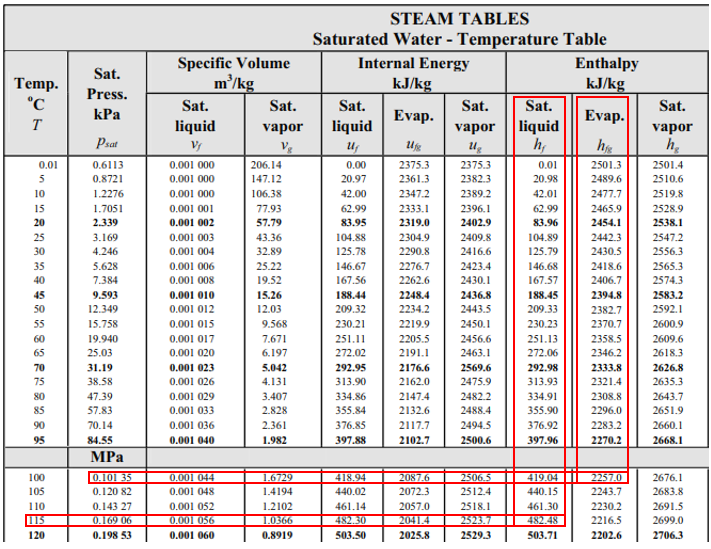
From the steam table at 115°C, the saturation pressure is 0.16906 MPa, and the enthalpy,
$$h_1$$
, is 482.48 kJ/kg (the problem states saturated water at 115°C). Because enthalpy does not change as liquid passes through a throttling valve,
$$h_1=h_2=482.48\:kJ/kg$$
. In the steam table again, 0.1035 MPa correlates to
$$T=100°C$$
,
$$h_f=419.04\:kJ/kg$$
and
$$h_{fg}=2257\:kJ/kg$$
.
Thus, for our problem statement:
$$$h_1=h_f+xh_{fg}$$$
$$$482.48\frac{kJ}{kg}=419.04\frac{kJ}{kg}+x(2257\frac{kJ}{kg})$$$
$$$x=\frac{63.44}{2257}=0.028$$$
0.028
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Throttling Valve