Temperature Probe
Consider a temperature probe, with the below controlling equation and a time constant of 5 seconds, is stuck inside a cup of liquid. What is the minimum time required before the probe indicates a temperature within ±2°C of the actual liquid temperature if the actual liquid and reference temperatures are 150°C and 50°C respectively?
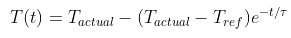
Expand Hint
Minimum time required means:
$$$T(t)=T_{actual}-2^{\circ}C=150^{\circ}C-2^{\circ}C=148^{\circ}C$$$
Hint 2
Solve for t:
$$$148^{\circ}C=150^{\circ}C-(150^{\circ}C-50^{\circ}C)e^{-t/5s}$$$
Minimum time required means:
$$$T(t)=T_{actual}-2^{\circ}C=150^{\circ}C-2^{\circ}C=148^{\circ}C$$$
Thus, we can solve for the minimum time (t):
$$$148^{\circ}C=150^{\circ}C-(150^{\circ}C-50^{\circ}C)e^{-t/5s}$$$
$$$(100^{\circ}C)e^{-t/5s}=150^{\circ}C-148^{\circ}C$$$
$$$e^{-t/5s}=\frac{2^{\circ}C}{100^{\circ}C}=0.02$$$
$$$ln[e^{-t/5s}]=ln[0.02]$$$
$$$\frac{-t}{5s}=-3.912$$$
$$$t=3.912(5s)=19.56\:sec$$$
19.56 s
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Temperature Sensors
270. Resistance Temperature Detector
292. RTD Element
496. RTD
Similar Problems from FE Section: Measurement
138. Electrical Signals
270. Resistance Temperature Detector
292. RTD Element
496. RTD