Uncertainty
Consider a resistance temperature detector (RTD) is made from platinum, and has a resistance, R, of 115 ohms, and a resistance at reference temperature (0°C) of 100 ohms. Using the below simplified Kline-McClintock equation, what is the temperature uncertainty if the resistance uncertainty is ±0.1 ohms? Note the resistance temperature coefficient for platinum is 0.004°C^(-1).
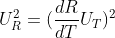
Expand Hint
$$$U_{R}^{2}=(\frac{dR}{dT}U_{T})^2$$$
where
$$U_R$$
is the resistance uncertainty,
$$dR$$
is the change in resistance,
$$dT$$
is the change in temperature, and
$$U_T$$
is the uncertainty in temperature.
Hint 2
$$$R_T=R_0[1+\alpha (T-T_0)]$$$
where
$$R_T$$
is the RTD’s resistance at temperature
$$T$$
,
$$R_0$$
is the RTD’s resistance at the reference temperature
$$T_0$$
(usually 0°C), and
$$\alpha$$
is the resistance temperature coefficient.
Resistance Temperature Detector (RTD) is a device used to relate change in resistance to change in temperature. They are typically made from platinum, and have the controlling equation:
$$$R_T=R_0[1+\alpha (T-T_0)]$$$
where
$$R_T$$
is the RTD’s resistance at temperature
$$T$$
,
$$R_0$$
is the RTD’s resistance at the reference temperature
$$T_0$$
(usually 0°C), and
$$\alpha$$
is the resistance temperature coefficient. First, solve for
$$T$$
:
$$$115\Omega=100\Omega[1+0.004^{\circ}C^{-1}(T-0^{\circ}C)]$$$
$$$1.15=1+0.004^{\circ}C^{-1}(T)$$$
$$$T=\frac{0.15}{0.004^{\circ}C^{-1}}=37.5^{\circ}C$$$
With
$$T=37.5^{\circ}C$$
, we now know everything to solve for the temperature uncertainty. Rearranging the simplified Kline-McClintock equation:
$$$U_{T}=\frac{U_{R}(dT)}{dR}$$$
where
$$U_R$$
is the resistance uncertainty,
$$dR$$
is the change in resistance,
$$dT$$
is the change in temperature, and
$$U_T$$
is the uncertainty in temperature.
$$$U_{T}=\frac{0.1\Omega(37.5^{\circ}C-0^{\circ}C)}{115\Omega-100\Omega}=\frac{0.1(37.5^{\circ}C)}{15}=0.25^{\circ}C$$$
0.25°C
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Temperature Sensors, Measurement Uncertainty
Similar Problems from FE Section: Measurement, Propagation of Error