Matrix Inverse
What is the inverse of the shown matrix?
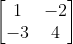
Expand Hint
The inverse of a square
$$n\times n$$
matrix is:
$$$A^{-1}=\frac{adj(A)}{|A|}$$$
where
$$|A|$$
is the determinant of matrix A, and
$$adj(A)$$
is the adjoint of matrix A, which is obtained by replacing
$$A^T$$
elements with their cofactors.
Hint 2
$$$\begin{bmatrix}a & b\\ c & d\end{bmatrix}^{-1}=\frac{1}{ad-bc}\begin{bmatrix}d & -b\\ -c & a\end{bmatrix}$$$
The inverse of a square
$$n\times n$$
matrix is:
$$$A^{-1}=\frac{adj(A)}{|A|}$$$
where
$$|A|$$
is the determinant of matrix A, and
$$adj(A)$$
is the adjoint of matrix A, which is obtained by replacing
$$A^T$$
elements with their cofactors. Thus, for a 2 x 2 matrix:
$$$\begin{bmatrix}a & b\\ c & d\end{bmatrix}^{-1}=\frac{1}{ad-bc}\begin{bmatrix}d & -b\\ -c & a\end{bmatrix}$$$
Therefore,
$$$\begin{bmatrix}1 & -2\\ -3 & 4\end{bmatrix}^{-1}=\frac{1}{(1)(4)-(-2)(-3)}\begin{bmatrix}4 & 2\\ 3 & 1\end{bmatrix}$$$
$$$=\frac{1}{4-6}\begin{bmatrix}4 & 2\\ 3 & 1\end{bmatrix}=-\frac{1}{2}\begin{bmatrix}4 & 2\\ 3 & 1\end{bmatrix}=\begin{bmatrix}-2 & -1\\ -1.5 & -0.5\end{bmatrix}$$$
The solution can be verified by multiplying the original matrix with its inverse. The resultant is the identity matrix (
$$n\times n$$
matrix with 1’s on the diagonal and 0’s everywhere else).
$$$[A][A]^{-1}=[A]^{-1}[A]=[I]$$$
where
$$[I]$$
is the identity matrix,
$$[A]$$
is the original matrix, and
$$[A]^{-1}$$
is the inverse matrix.
$$$\begin{bmatrix}-2 & -1\\ -1.5 & -0.5\end{bmatrix}$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Inverse
511. Inverse Matrix
548. Inverse of Matrix
Similar Problems from FE Section: Matrices
277. Matrix Transpose
279. Matrix Multiplication
507. Transpose Matrix
509. Transpose Size
511. Inverse Matrix
518. Matrix Multiply
548. Inverse of Matrix