Centroid Area
For the shown figure, what is the y-coordinate of the centroid in m? Note the figure is not drawing to scale.
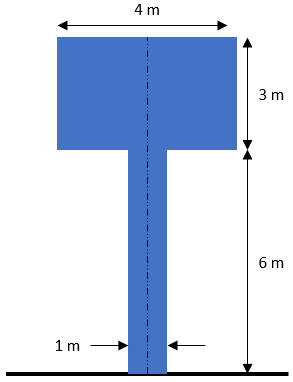
Expand Hint
Split the object into basic shapes (triangles, rectangles, squares, etc.).
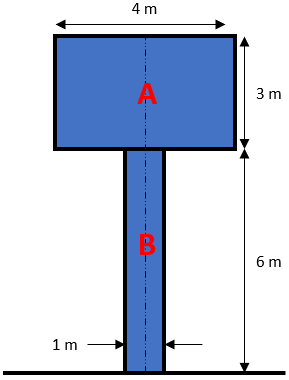
Hint 2
The y-component of an area’s centroid is defined as:
$$$y_{ac}=\frac{\sum y_n a_n}{A}$$$
where
$$a_n$$
is the simplified object’s area,
$$y_n$$
is the distance from the origin to the middle of the simplified object, and
$$A$$
is the total area.
The y-component of an area’s centroid is defined as:
$$$y_{ac}=\frac{\sum y_n a_n}{A}$$$
where
$$a_n$$
is the simplified object’s area,
$$y_n$$
is the distance from the origin to the middle of the simplified object, and
$$A$$
is the total area (
$$\Sigma a_n$$
).
First, let’s split the main object into basic shapes (triangles, rectangles, squares, etc.).
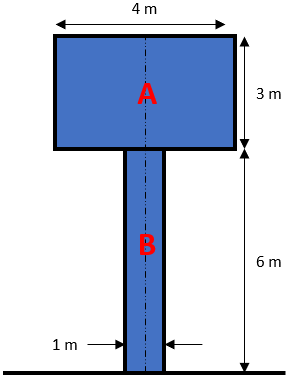
To find the y-component of the main object’s centroid, let’s set the ground as the origin:
$$$y_{ac}=\frac{(y_A a_A)+(y_B a_B)}{(a_A+a_B)}=\frac{[(\frac{3m}{2}+6m)(4m\cdot 3m)]+[\frac{6m}{2}\cdot(6m\cdot 1m)]}{[(4m\cdot 3m)+(6m\cdot 1m)]}$$$
$$$=\frac{[(7.5m)(12m^2)+(3m)(6m^2)]}{(12m^2+6m^2)}=\frac{(90m^3+18m^3)}{18m^2}=\frac{108m^3}{18m^2}=6\:m$$$
6 m
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Centroid of Area
614. Y Centroid
Similar Problems from FE Section: Centroids of Masses, Areas, Lengths, and Volumes
614. Y Centroid