Interest Rate Table
Using the interest rate table below, how much money would have accrued after 5 years if $2,000 is invested now at 10% compounded annually?
Expand Hint
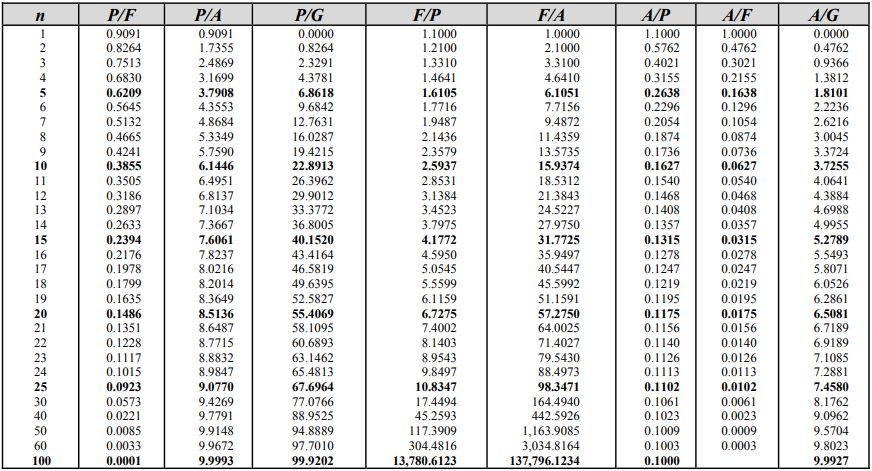
The problem statement is asking for growth after 5 years, so
$$n=5$$
:
Hint 2
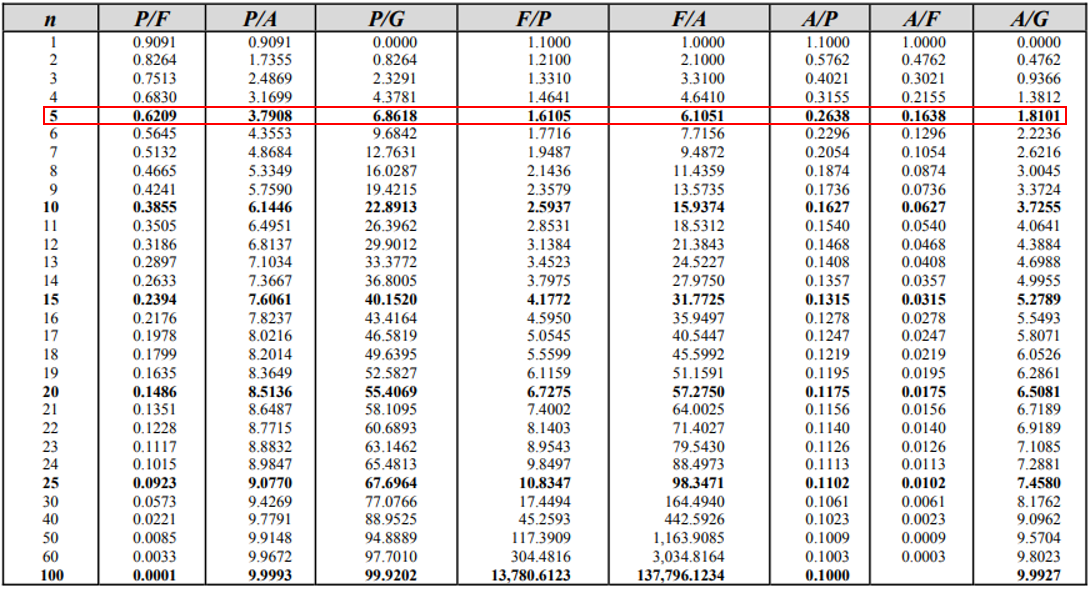
We are trying to solve for the Future,
$$F$$
, given the present value,
$$P$$
, of $2,000.
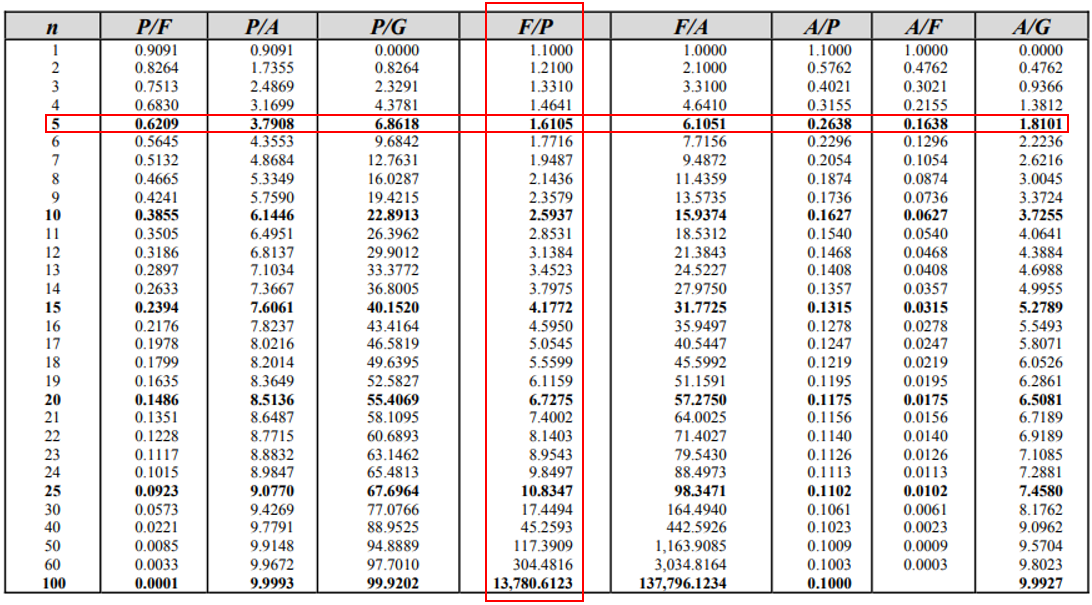
The problem statement is asking for a single payment based on a compounded amount. Based on the givens:
$$n$$
, the number of compounding periods, is 5. We are trying to solve for the Future,
$$F$$
, given the present value,
$$P$$
, which converts to
$$F\:given\:P$$
.
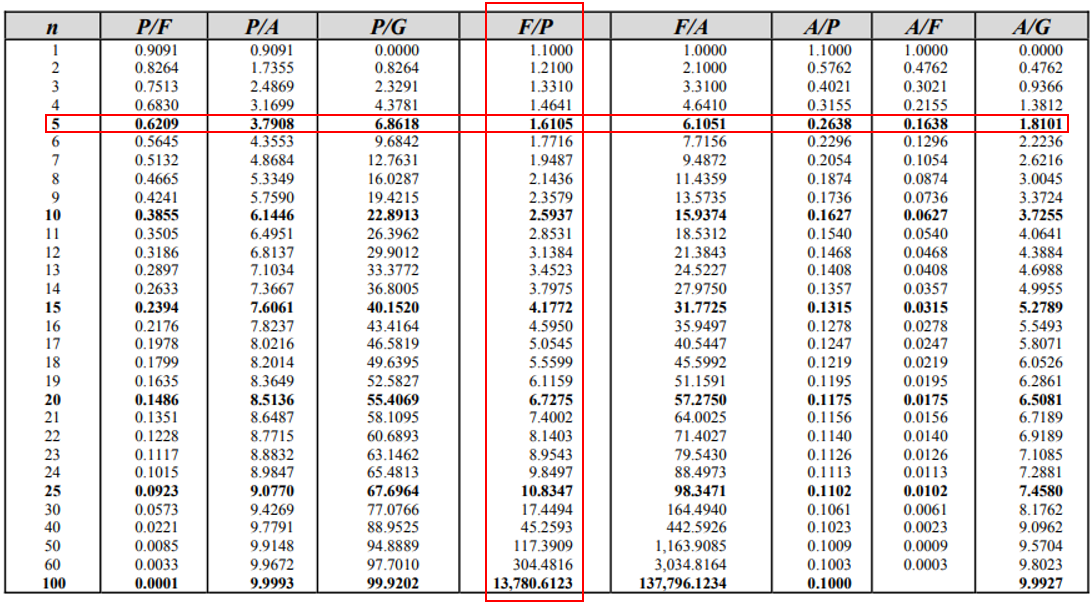
The intersection value, 1.6105, from the 10% Interest Rate Table is the compounding factor. Thus, the initial investment will grow into:
$$$Future=Present \times Factor$$$
$$$Future=\$2,000 \times 1.6105=\$3,221$$$
Note, we can check our answer with the below formula:
$$$(1+i)^n=(1+0.1)^5=(1.1)^5=1.6105$$$
where
$$i$$
is the interest rate, and
$$n$$
is the number of compounding periods. Because our compounding factor matches with the table, we confirmed that our initial answer is correct.
$3,221
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Single Payment Compound Amount
144. Interest
377. Investment Growth
551. Bond
Similar Problems from FE Section: Nomenclature and Definitions
117. Housing Down Payment
142. Saving for the Future
144. Interest
324. Simple Interest
377. Investment Growth
551. Bond
581. Savings
632. Down Payment
657. Landing Gear