Mass Moment of Inertia
For the point mass figure below, what is the mass moment of inertia?
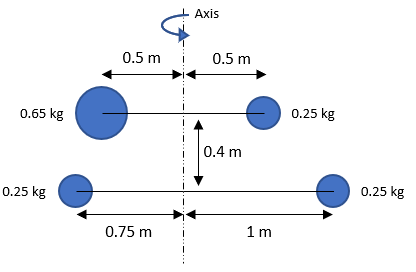
Expand Hint
For point masses, the mass moment of inertia is:
$$$I=\sum m_ir_i^2$$$
where
$$m$$
is the mass, and
$$r$$
is the perpendicular distance to the rotation axis.
Hint 2
Ignore the 0.4 m distance. That dimension is there to throw you off.
For point masses, the mass moment of inertia is:
$$$I=\sum m_ir_i^2$$$
where
$$m$$
is the mass, and
$$r$$
is the perpendicular distance to the rotation axis.
The figure has four point masses:
$$$I=m_1r_{1}^{2}+m_2r_{2}^{2}+m_3r_{3}^{2}+m_4r_{4}^{2}$$$
Remember,
$$r$$
is the perpendicular distance the mass is from the rotation axis, not parallel distance, meaning the 0.4 m dimension is there for confusion and can be ignored. Starting from the bottom right point mass and moving clockwise:
$$$I=(0.25kg)(1m)^{2}+(0.25kg)(0.75m)^{2}+(0.65kg)(0.5m)^{2}+(0.25kg)(0.5m)^{2}$$$
$$$=(0.25kg)(1m^2)+(0.25kg)(0.5625m^2)+(0.65kg)(0.25m^2)+(0.25kg)(0.25m^2)$$$
$$$=0.25kg\cdot m^2+0.140625kg\cdot m^2+0.1625kg\cdot m^2+0.0625kg\cdot m^2$$$
$$$I=0.616\:kg\cdot m^2$$$
$$$0.616\:kg\cdot m^2$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Mass Moment of Inertia
034. A Robotic Arm
334. Mass Moments
631. Robotic Arm
Similar Problems from FE Section: Plane Motion of a Rigid Body
034. A Robotic Arm
330. Figure Skating
334. Mass Moments
631. Robotic Arm