Moment of a Force
In the below figure, a freely rotating pulley is acted on by two forces. Determine the magnitude for the second force that would make the pulley be in rotational equilibrium.
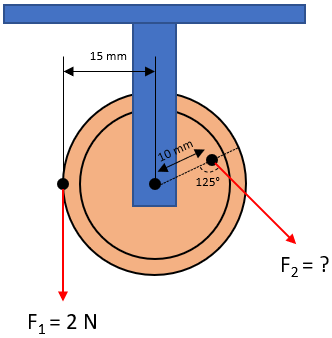
Expand Hint
The question is asking for
$$$F_1=F_2$$$
More specifically, the question is asking for the toques/moments to be equal.
$$$\tau_1=\tau_2$$$
Hint 2
Torque:
$$$\tau=F\cdot rsin(\theta) $$$
where
$$F$$
is the force,
$$r$$
is the length of the moment arm, and
$$\theta$$
is the angle between the force vector and moment arm.
The question is asking for
$$$F_1=F_2$$$
More specifically, the question is asking for the toques/moments to be equal.
$$$\tau_1=\tau_2$$$
Remember, to find torque:
$$$\tau=F\cdot rsin(\theta) $$$
where
$$F$$
is the force,
$$r$$
is the length of the moment arm, and
$$\theta$$
is the angle between the force vector and moment arm.
First, let’s analyze the torque/moment for the first force since there aren’t any unknown variables:
$$$\tau_1=(2N)\cdot (0.015m)sin(90^{\circ}) =(2N)(0.015m)(1)=0.03\:N\cdot m$$$
Now that both torques are known, let’s solve for
$$F_2$$
using the same equation:
$$$\tau_1=\tau_2=F_2\cdot (0.01m)sin(125^{\circ})=0.03\:N\cdot m$$$
$$$F_2=\frac{0.03N\cdot m}{(0.01m)(0.819)}$$$
$$$F_2=\frac{0.03N\cdot m}{(0.01m)(0.819)}=\frac{0.03N\cdot m}{0.00819m}=3.66\:N$$$
3.66 N
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Force, Moment
Similar Problems from FE Section: Force, Moments (Couples)