Drainage Time
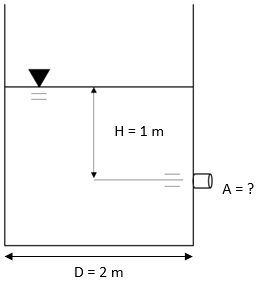
The figure shown is a cross sectional view of a circular water tank with a 2 m diameter that discharges water freely into the atmosphere. If the time required to drain the water line from 1 m to 0.5 m is 1 minute, what is the output nozzle’s cross-sectional area in square cm? Assume no minor losses in discharge.
Expand Hint
The time required to drain a circular tank:
$$$\Delta t=\frac{2(A_t/A_0)}{\sqrt{2g}}(h_{1}^{0.5}-h_{2}^{0.5})$$$
where
$$A_t$$
is the tank’s cross-sectional area,
$$A_0$$
is the cross-sectional area of fluid flow,
$$g$$
is the acceleration due to gravity,
$$h_1$$
is the initial fluid line height, and
$$h_2$$
is the final fluid line height.
Hint 2
$$$A_t=\frac{\pi D_{t}^{2}}{4}$$$
where
$$D_t$$
is the circular tank’s diameter.
First, let’s find the tank’s cross-sectional area:
$$$A_t=\frac{\pi D_{t}^{2}}{4}$$$
where
$$D_t$$
is the circular tank’s diameter.
$$$A_t=\frac{\pi (2m)^{2}}{4}=3.14\:m^2$$$
The time required to drain a circular tank:
$$$\Delta t=\frac{2(A_t/A_0)}{\sqrt{2g}}(h_{1}^{0.5}-h_{2}^{0.5})$$$
where
$$A_t$$
is the tank’s cross-sectional area,
$$A_0$$
is the cross-sectional area of fluid flow,
$$g$$
is the acceleration due to gravity,
$$h_1$$
is the initial fluid line height, and
$$h_2$$
is the final fluid line height.
$$$1min\cdot \frac{60sec}{1min}=\frac{2(3.14m^2/A_0)}{\sqrt{2(9.8m/s^2)}}((1m)^{0.5}-(0.5m)^{0.5})$$$
Solving for the nozzle’s cross-sectional area:
$$$60sec=\frac{2(3.14m^2/A_0)}{\sqrt{19.6m/s^2}}(1\sqrt{m}-0.707\sqrt{m})$$$
$$$60s=\frac{2(3.14m^2/A_0)}{4.43\frac{\sqrt{m}}{s}}(0.293\sqrt{m})$$$
$$$\frac{60s(4.43s^{-1})}{(0.293)}=\frac{6.28m^2}{A_0}$$$
$$$A_0=\frac{6.28m^2}{907.17}=0.0069m^2=69\:cm^2$$$
$$$69\:cm^2$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Orifice Discharging Freely into Atmosphere
087. Water Tank
431. Discharging Orifice
435. Time to Drain
Similar Problems from FE Section: Characteristics of Selected Flow Configurations
087. Water Tank
300. Water Velocity
368. Elevated Storage Tank
431. Discharging Orifice
435. Time to Drain
459. Submerged Orifice
464. Submerged Tank
472. Water Slope
566. Pipe Slope
606. Roughness Coefficient
638. Velocity of Water