Low Pass Filters
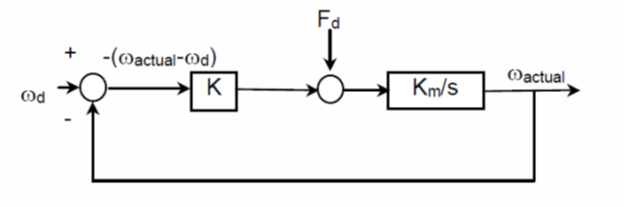
Refer to the below diagram to answer the following questions.
- Derive an expression that relates w(actual) to w(d) and F(d).
- Explain why high-gain feedback (i.e. a big proportional gain K) was able to better cancel the effects of friction on the motor shaft and make the motor spin at a speed closer to the desired velocity.
- Derive the transfer function of the closed-loop system shown in the block diagram.
- What type of filter does this transfer function resemble? What is its constant? Recall that transfer functions are found by setting all inputs and disturbances to zero.
Expand Hint
The control law relating K and ω is given by:
$$$F=K(\omega _{d}-\omega)$$$
Hint 2
To derive the transfer function, solve for
$$\frac{\omega}{\omega_d}$$
The control law relating K and ω is given by:
$$$F=K(\omega _{d}-\omega)$$$
Adding the disturbance force we then have:
$$$\omega=[K(\omega _{d}-\omega)+F_d]\frac{K_m}{S}\rightarrow \frac{KK_m}{S}\omega_d+\frac{K_m}{s}F_d=\omega + \frac{KK_m}{s}\omega=\omega*\frac{(S+KK_m)}{S}$$$
$$$\omega=\frac{KK_m}{S+KK_m}\omega_d+\frac{K_m}{S+KK_m}F_d$$$
Therefore, if K is large, then the effect from the disturbance force is effectively cancelled and
$$\omega$$
~
$$\omega_d$$
Setting the disturbance to zero, we have:
$$$\omega=\frac{K_m}{S}K(\omega_d-\omega)$$$
$$$\frac{\omega}{\omega_d}=\frac{KK_m}{S+KK_m}=\frac{1}{\frac{1}{KK_m}+1}$$$
The system’s time constant is given by:
$$\tau =1/KK_m$$
The transfer function is similar to that of a low pass filter.
- $$\omega=\frac{KK_m}{S+KK_m}\omega_d+\frac{K_m}{S+KK_m}F_d$$
- If K is large, then the effect from the disturbance force is effectively cancelled and $$\omega$$ ~ $$\omega_d$$
- $$\frac{\omega}{\omega_d}=\frac{KK_m}{S+KK_m}=\frac{1}{\frac{1}{KK_m}+1}$$
- The transfer function is similar to that of a low pass filter. The system’s time constant is given by: $$\tau =1/KK_m$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked