Differential Equations & Filters
The below diagram is an RC circuit being used as a low-pass filter in order to filter a PWM signal generated by a microcontroller. Use Kirchhoff’s voltage law to find the first-order differential equation that relates the voltage across the capacitor (Vout) to Vin, R, and C.
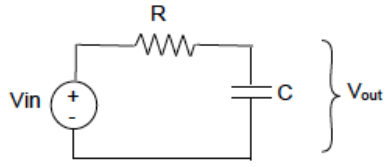
Expand Hint
KVL:
$$$V_{in}-Ri-V_{out}=0$$$
where
$$V$$
is the voltage,
$$i$$
is the current, and
$$R$$
is the resistance.
Hint 2
Ohm's Law:
$$$V=IR$$$
where
$$V$$
is the voltage,
$$I$$
is the current, and
$$R$$
is the resistance.
Using KVL we have:
$$$V_{in}-Ri-V_{out}=0$$$
where
$$V$$
is the voltage,
$$i$$
is the current, and
$$R$$
is the resistance. We also know that for a capacitor we have:
$$$C\frac{dv}{dt}=i$$$
Applying Ohm’s Law:
$$$V=IR=RC\frac{dV_{out}}{dt}$$$
Since the current throughout the circuit must be the same, we can write KVL as:
$$$V_{in}-RC\frac{dV_{out}}{dt}-V_{out}=0$$$
$$$V_{out}=V_{in}-RC\frac{dV_{out}}{dt}$$$
$$$V_{out}=V_{in}-RC\frac{dV_{out}}{dt}$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked