Lever Arm
In the lever arm below, calculate the moment force (F) causes on Point A.

Expand Hint
The diagonal force applied at the end of the lever arm can be broken down into a
$$F_x$$
component.
$$$F_x=F\cdot cos(\theta)$$$
Hint 2
The diagonal force applied at the end of the lever arm can be broken down into a
$$F_y$$
component.
$$$F_y=F\cdot sin(\theta)$$$
The diagonal force applied at the end of the lever arm can be broken down into
$$F_x$$
and
$$F_y$$
components.
$$$F_x=F\cdot cos(\theta)=700\cdot cos(30)=606.22\:N$$$
$$$F_y=F\cdot sin(\theta)=700\cdot sin(30)=350\:N$$$
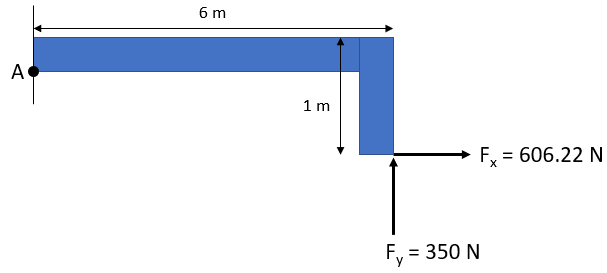
A system of two forces that are equal in magnitude, opposite in direction, and parallel to each other is called a couple. A moment (M) is defined as the cross product of the radius vector (r) and the force (f) from a point to the force's line of action.
$$$M=r \times F$$$
$$$M_z=xF_y-yF_x$$$
Thus, the moment about Point A:
$$$M_A=(6m)(350N)-(1m)(606.22N)=2100-606.22=1494\:N\cdot m$$$
$$$1494\:N\cdot m$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked