Pendulum
If a pendulum with a 2 kg mass at the end is released from rest at Position A in the diagram below, what is the mass's velocity at Position B? Ignore friction.

Expand Hint
Law of Conservation of Energy:
$$$KE_1+PE_1=KE_2+PE_2$$$
where
$$KE_1$$
is the initial kinetic energy,
$$PE_1$$
is the initial potential energy,
$$KE_2$$
is the final kinetic energy, and
$$PE_2$$
is the final potential energy.
Hint 2
Kinetic Energy is:
$$KE=1/2mv^2$$
, where
$$m$$
is the mass and
$$v$$
is the velocity. Potential Energy is:
$$PE=mgh$$
, where
$$m$$
is the mass,
$$g$$
is the acceleration due to gravity, and
$$h$$
is the height.
Because there is no heat loss due to friction, the law of conservation of energy is:
$$$KE_1+PE_1=KE_2+PE_2$$$
where
$$KE_1$$
is the initial kinetic energy,
$$PE_1$$
is the initial potential energy,
$$KE_2$$
is the final kinetic energy, and
$$PE_2$$
is the final potential energy.
In our scenario, our mass starts at rest in Position A, so initial kinetic energy is zero, while potential energy is at max. At Position B, potential energy is zero, while kinetic energy is at max. Since
$$KE=1/2mv^2$$
and
$$PE=mgh$$
, our equation is:
$$$0+mgh_1=\frac{1}{2}mv_{2}^{2}+0$$$
$$$h_1(9.8m/s^2)=\frac{1}{2}v_{2}^{2}$$$
since we are solving for
$$v_2$$
, all we need to determine is the height difference between Position A and Position B.
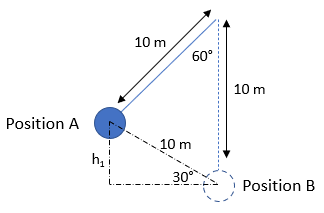
$$$sin(30)=\frac{h_1}{10}\rightarrow h_1=10sin(30)=5\:m$$$
Thus,
$$$v_2=\sqrt{(2)(5m)(9.8m/s^2)}=\sqrt{98m^2/s^2}=9.9\:m/s$$$
9.9 m/s
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked