Two Black Surfaces
Consider the cubic enclosure below has an area of 2 m^2 for each face. Surface 1, which refers to the bottom black face, has a temperature of 600°C. Surface 2, which refers to the back black face, has a temperature of 450°C. If the shape factor between the two surfaces is 0.3, what is the net heat transfer rate caused by radiation in kW? Note the Stefan-Boltzmann constant is 5.67 x 10^8W/(m^2*K^4).
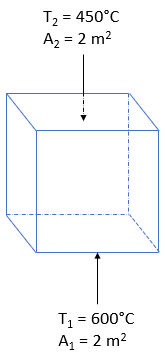
Expand Hint
The net energy exchange by radiation between two black bodies that see each other is:
$$$Q_{1-2}=\sigma A_1F_{1-2}(T_{1}^{4}-T_{2}^{4})$$$
where
$$\sigma$$
is the Stefan-Boltzmann constant [
$$\sigma = 5.67\times 10^{-8}W/(m^2\cdot K^4)$$
],
$$A$$
is the body surface area,
$$F$$
is the shape factor,
$$T_1$$
is the absolute temperature of the body surface, and
$$T_2$$
is the absolute temperature of the surroundings.
Hint 2
To convert from Celsius to Kelvin, add 273 to the temperature in Celsius.
The net energy exchange by radiation between two black bodies that see each other is:
$$$Q_{1-2}=\sigma A_1F_{1-2}(T_{1}^{4}-T_{2}^{4})$$$
where
$$\sigma$$
is the Stefan-Boltzmann constant [
$$\sigma = 5.67\times 10^{-8}W/(m^2\cdot K^4)$$
],
$$A$$
is the body surface area,
$$F$$
is the shape factor,
$$T_1$$
is the absolute temperature of the body surface, and
$$T_2$$
is the absolute temperature of the surroundings.
$$$Q_{1-2}= 5.67\times 10^{-8}\frac{W}{(m^2\cdot K^4)}(2m^2)(0.3)[(600+273K)^4-(450+273K)^4]$$$
$$$Q_{1-2}= 10,464.38\:W=10.46\:kW$$$
10.46 kW
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Net Energy Exchange by Radiation between Two Bodies
Similar Problems from FE Section: Radiation
285. Internet Cable