Internet Cable
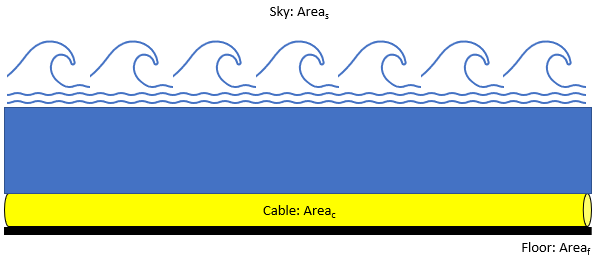
Below is a side view figure of a 70 mm thick fiber optic cable laid out on the ocean floor bottom. Since this cable is providing internet between European and American servers, assume an infinitely large sky and ocean floor, and an infinitely long cable. If the shape factor between the cable’s surface area and the ocean floor’s surface area is 3/4, what is the shape factor between the cable and sky’s surface areas?
Expand Hint
Summation Rule for
$$N$$
Surfaces:
$$$\sum_{j=1}^{N}F_{ij}=1$$$
where
$$F_{ij}$$
is the shape factor;
$$0\leq F_{ij}\leq 1$$
Hint 2
Shape factor is the fraction of radiation that leaves from surface
$$i$$
and strikes surface
$$j$$
.
Shape factor is the fraction of radiation that leaves from surface
$$i$$
and strikes surface
$$j$$
. Summation Rule for
$$N$$
Surfaces:
$$$\sum_{j=1}^{N}F_{ij}=1$$$
where
$$F_{ij}$$
is the shape factor;
$$0\leq F_{ij}\leq 1$$
In the problem statement, we have three surfaces (Ocean Floor, Cable, and Sky), which implies that there are also three surfaces to receive radiation. Thus,
$$$\sum_{j=1,2,3}^{3}F_{ij}=1=F_{i1}+F_{i2}+F_{i3}$$$
In our case,
$$i$$
is the cable because it is radiating heat, and
$$1,2,3$$
are the surfaces:
$$$F_{cable,floor}+F_{cable,sky}+F_{cable,cable}=1$$$
$$F_{cable,floor}$$
is given, and
$$F_{cable,cable}$$
is zero because it cannot intercept radiation from its own surface. Therefore,
$$$\frac{3}{4}+F_{cable,sky}+0=1$$$
$$$F_{cable,sky}=1-\frac{3}{4}=\frac{1}{4}$$$
1/4
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Shape Factor (View Factor, Configuration Factor) Relations
Similar Problems from FE Section: Radiation
226. Two Black Surfaces