Hyperbola
What is the eccentricity of the conic section represented by the below equation?
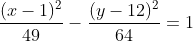
Expand Hint
The equation for a hyperbola has the below format:
$$$\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1$$$
Hint 2
Eccentricity:
$$$e=\sqrt{1+(b^2/a^2)}$$$
A conic section is a curve obtained from the intersection of a cone’s surface and a flat plane. The eccentricity,
$$e$$
, of a conic section indicates how close its shape is a circle. As eccentricity grows larger, the less the shape resembles a circle. The problem’s equation is a hyperbola because it has the below format:
$$$\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1$$$
Note the similarities to an ellipse equation, except the two components are being subtracted instead of added. The eccentricity,
$$e$$
, of a conic section indicates how close its shape is a circle. To solve for eccentricity:
$$$e=\sqrt{1+(b^2/a^2)}$$$
Thus,
$$$e=\sqrt{1+(64/49)}=\sqrt{1+1.306}=\sqrt{2.306}=1.52$$$
1.52
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Conic Sections
129. General Forms
282. Conic Shapes
283. Eccentricity
340. Zero Eccentricity
448. Ellipse
471. Greater Eccentricity
Similar Problems from FE Section: Mensuration of Areas and Volumes
129. General Forms
282. Conic Shapes
283. Eccentricity
340. Zero Eccentricity
448. Ellipse
471. Greater Eccentricity