Ellipse
What is the eccentricity of the conic section represented by the below equation?
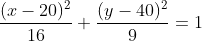
Expand Hint
The equation for an ellipse has the below format:
$$$\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$$$
Hint 2
Eccentricity:
$$$e=\sqrt{1-(b^2/a^2)}$$$
A conic section is a curve obtained from the intersection of a cone’s surface and a flat plane. The eccentricity,
$$e$$
, of a conic section indicates how close its shape is a circle. As eccentricity grows larger, the less the shape resembles a circle. The problem’s equation is an ellipse because it has the below format:
$$$\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$$$
The eccentricity,
$$e$$
, of a conic section indicates how close its shape is a circle. To solve for eccentricity:
$$$e=\sqrt{1-(b^2/a^2)}$$$
Thus,
$$$e=\sqrt{1-(9/16)}=\sqrt{1-0.5625}=\sqrt{0.4375}=0.66$$$
0.66
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Conic Sections
129. General Forms
282. Conic Shapes
283. Eccentricity
284. Hyperbola
340. Zero Eccentricity
471. Greater Eccentricity
Similar Problems from FE Section: Mensuration of Areas and Volumes
129. General Forms
282. Conic Shapes
283. Eccentricity
284. Hyperbola
340. Zero Eccentricity
471. Greater Eccentricity