Beam Centroid
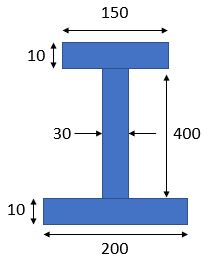
Calculate the centroid for the I-Beam cross section below.
Expand Hint
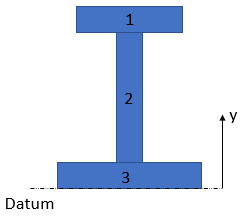
We can determine the centroid by breaking down the cross section into three segments, and setting a datum at the beam's bottom face (you could easily set the datum elsewhere like the top, or broken the segments into different areas):
Hint 2
To find the centroid:
$$$\bar{y}=\frac{\sum A_iy_i}{\sum A_i}$$$
where
$$A_i$$
is the individual segment's area, and
$$y_i$$
is the individual segment's centroid distance from a reference line or datum.
We can determine the centroid by breaking down the cross section into three segments, and setting a datum at the beam's bottom face (you could easily set the datum elsewhere like the top, or broken the segments into different areas):
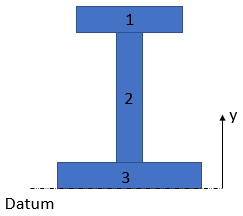
To find the centroid, we use the formula:
$$$\bar{y}=\frac{\sum A_iy_i}{\sum A_i}$$$
where
$$A_i$$
is the individual segment's area, and
$$y_i$$
is the individual segment's centroid distance from a reference line or datum.
Segment 1:
$$$A_1=150\times 10=1500$$$
$$$y_1=10+400+\frac{10}{2}=415$$$
Segment 2:
$$$A_2=30\times 400=12,000$$$
$$$y_2=10+\frac{400}{2}=210$$$
Segment 3:
$$$A_3=10\times 200=2000$$$
$$$y_3=\frac{10}{2}=5$$$
Thus,
$$$\bar{y}=\frac{A_1y_1+A_2y_2+A_3y_3}{A_1+A_2+A_3}$$$
$$$\bar{y}=\frac{(1,500)(415)+(12,000)(210)+(2,000)(5)}{(1,500+12,000+2,000)}$$$
$$$\bar{y}=\frac{622,500+2,520,000+10,000}{15,500}=\frac{3,152,500}{15,500}=203.4$$$
203.4
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked