Cross Bar
In the below diagram, a cross plane member has a 15 mm uniform thickness and some loads in compression/tension. What is the max shear stress at the origin?
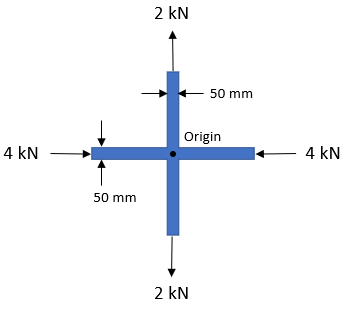
Expand Hint
Stress:
$$$\sigma = \frac{Load}{Area}$$$
Hint 2
The max shear stress considering three dimensions:
$$$\tau_{max}=\frac{\sigma_y-\sigma_x}{2}$$$
The stress at the origin can be represented as:
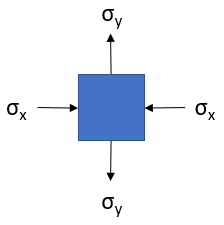
which looks like a typical Mohr's Circle problem. To construct a Mohr's circle, the following sign conventions are used:
Since
$$stress=\frac{load}{area}$$
$$$\sigma_x=\frac{4,000N}{(0.05m)(0.015m)}=-5.33\:MPa$$$
$$$\sigma_y=\frac{2,000N}{(0.05m)(0.015m)}=2.67\:MPa$$$
Since
$$\sigma_x$$
is compressive:
$$$\sigma_1=2.67\:MPa$$$
$$$\sigma_2=0\:MPa$$$
$$$\sigma_3=-5.33\:MPa$$$
The max shear stress considering three dimensions is always:
$$$\tau_{max}=\frac{\sigma_1-\sigma_3}{2}=\frac{2.67-(-5.33)}{2}=4\:MPa$$$
4 MPa
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked