Water Barrel Collision
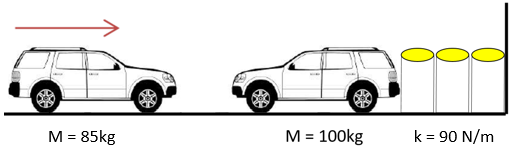
In the below figure, a 85 kg car collides with a 100 kg car that is at rest next to some water barrels you typically find on the highway. The barrels act as a spring between the vehicle and fixed wall to reduce impact. If the barrels have a spring constant of 90 kN/m, and the larger car is observed to have moved 6 m/s immediately after impact, what is the max acceleration of the 100 kg car after impact?
Expand Hint
The spring’s potential energy:
$$$U=\frac{kx^{2}}{2}$$$
where
$$k$$
is the spring constant, and
$$x$$
is the compressed distance.
Hint 2
The larger car's kinetic energy:
$$$KE=\frac{1}{2}mv^2$$$
where
$$m$$
is the mass, and
$$v$$
is the velocity.
The spring's potential energy:
$$$U=\frac{kx^{2}}{2}=\frac{90N(x)^2}{2\cdot m}=45(x)^2N/m$$$
where
$$k$$
is the spring constant, and
$$x$$
is the compressed distance. The larger car's kinetic energy:
$$$KE=\frac{1}{2}mv^2=\frac{1}{2}(100kg)(6m/s)^2=1,800\:N\cdot m$$$
where
$$m$$
is the mass, and
$$v$$
is the velocity. Because energy is conserved,
$$U=KE$$
$$$1,800N\cdot m=45(x)^2\frac{N}{m}$$$
$$$40m^2=(x)^2$$$
$$$x=\sqrt{40m^2}=6.325\:m$$$
The spring compressed 6.325 m when the larger car was observed travelling at 6 m/s. At max compression, the spring force is given by:
$$$F=kx=mass\times acceleration$$$
$$$(90N/m)(6.325m)=(100kg)\times a$$$
$$$a=\frac{569.2N}{100kg}=5.69\:\frac{m}{s^2}$$$
$$$5.69\:\frac{m}{s^2}$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Kinetic Energy
140. Conservation of Energy
166. Water Barrels
287. Kinetic Energy
361. Pinball Machine
364. Road Rash
526. K.E.
599. Formula 1 Energy
Similar Problems from FE Sub Section: Potential Energy
140. Conservation of Energy
166. Water Barrels
293. Pushing a Boulder
361. Pinball Machine
600. Towing a Trailer
Similar Problems from FE Section: Principle of Work and Energy
140. Conservation of Energy
166. Water Barrels
287. Kinetic Energy
293. Pushing a Boulder
361. Pinball Machine
364. Road Rash
526. K.E.
599. Formula 1 Energy
600. Towing a Trailer