Road Rash
Consider a 65 kg motorcyclist goes down on the road and slides horizontally across the rough asphalt. After sliding 20 m, his speed slows down to 6 m/s. If the kinetic coefficient of friction between his protective body armor and the road is 0.4, what initial speed did he fall at?
Expand Hint
Energy is not conserved:
$$$T_2+V_2=T_1+V_1+U_{1 \to 2}$$$
where
$$T$$
is the kinetic energy,
$$V$$
is the potential energy, and
$$U$$
is the work done by non-conservative forces in moving between state 1 and state 2.
Hint 2
Free body diagram:
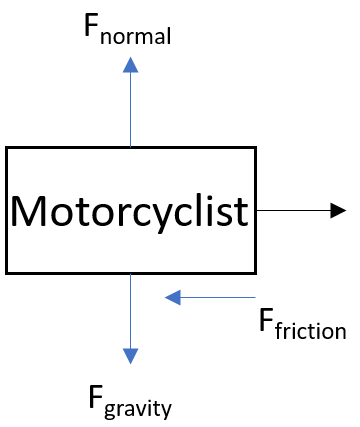
Friction is working against the motorcyclist (slowing him down as he slides across the asphalt), so energy is not conserved:
$$$T_2+V_2=T_1+V_1+U_{1 \to 2}$$$
where
$$T$$
is the kinetic energy,
$$V$$
is the potential energy, and
$$U$$
is the work done by non-conservative forces in moving between state 1 and state 2. It’s important to track the algebraic sign of the work term. If the forces serve to increase the energy of the system, then work is positive. If the forces, such as friction, dissipate energy, then work is negative.
Drawing the free body diagram:
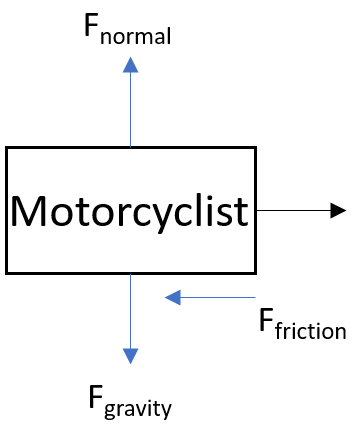
Work is negative because friction is slowing down the motorcyclist.
The friction force is:
$$$f=\mu N=\mu \times mg$$$
where
$$\mu$$
is the friction coefficient,
$$N$$
is the normal force,
$$m$$
is the mass, and
$$g$$
is the acceleration due to gravity.
Work is:
$$$U=Force\times Distance$$$
Thus, the work done by the friction force is:
$$$U_f=\mu \times mg \times x=(0.4)(65kg)(9.8m/s^2)(20m)=5,096\:N \cdot m$$$
Based on the problem statement:
- $$T_1$$ is the kinetic energy right before the rider falls.
- $$V_1=0$$ because potential energy is non-existent in this scenario.
- $$V_2=0$$ because potential energy is non-existent in this scenario.
- $$T_2$$ is the kinetic energy of the rider after he slides 20 m across the asphalt.
Remember, kinetic energy is:
$$$T=\frac{1}{2}mv^2$$$
where
$$m$$
is the mass and
$$v$$
is the velocity.
Therefore,
$$$\frac{1}{2}mv_2^2=\frac{1}{2}mv_1^2-U_f$$$
$$$\frac{1}{2}(65kg)(6m/s)^2=\frac{1}{2}(65kg)v_1^2-5,096N \cdot m$$$
$$$1,170N\cdot m+5,096N \cdot m=\frac{1}{2}(65kg)v_1^2$$$
$$$v_1^2=\frac{(2)\times 6,266N \cdot m}{65kg}=192.8m^2/s^2$$$
$$$v_1=\sqrt{192.8m^2/s^2}=13.89\:m/s$$$
13.89 m/s
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Kinetic Energy
140. Conservation of Energy
166. Water Barrels
238. Water Barrel Collision
287. Kinetic Energy
361. Pinball Machine
526. K.E.
599. Formula 1 Energy
Similar Problems from FE Sub Section: Work
361. Pinball Machine
Similar Problems from FE Section: Principle of Work and Energy
140. Conservation of Energy
166. Water Barrels
238. Water Barrel Collision
287. Kinetic Energy
293. Pushing a Boulder
361. Pinball Machine
526. K.E.
599. Formula 1 Energy
600. Towing a Trailer