Angular Acceleration
Consider a 0.25 m radius wheel rotates about a frictionless axle in its center, and has a mass moment of inertia of 0.055 kg*m^2. If a 2 kg mass hangs off the wheel's side by a massless cord wrapped around the cylinder without slip, what is the wheel's angular acceleration?

Expand Hint
$$$\sum M_{center}=I_{center}\times \alpha$$$
where
$$\alpha$$
is the angular acceleration both about an axis normal to the plane of motion,
$$I$$
is the mass moment of inertia about the normal axis through the mass center, and
$$M$$
is the moment.
Hint 2
First, let's create the free body diagram and solve for the sum of forces in the y-direction:
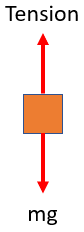
$$$\sum F_y=mass \times acceleration$$$
First, let's create the free body diagram and solve for the sum of forces in the y-direction:
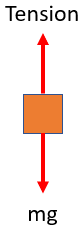
$$$\sum F_y=mass \times acceleration$$$
$$$mg-T=ma$$$
Because there is no slip:
$$a=\alpha r$$
$$$mg-T=m\alpha r$$$
$$$(2kg)(9.8m/s^2)-T=(2kg)\alpha (0.25m)$$$
$$$T=(19.6kg\cdot m/s^2)-\alpha (0.5kg\cdot m)$$$
In general, Newton's second law for a rigid body, with constant mass and mass moment of inertia, in plane motion may be written in vector form as
$$$\sum M_{center}=I_{center}\times \alpha$$$
where
$$\alpha$$
is the angular acceleration both about an axis normal to the plane of motion,
$$I$$
is the mass moment of inertia about the normal axis through the mass center, and
$$M$$
is the moment. Since
$$M=force \times distance$$
:
$$$T(0.25m)=(0.055kg\cdot m^2)(\alpha)$$$
$$$[(19.6kg\cdot m/s^2)-\alpha (0.5kg\cdot m)](0.25m)=(0.055kg\cdot m^2)(\alpha)$$$
$$$(4.9kg\cdot m^2\cdot s^{-2})-\alpha (0.125kg\cdot m^2)=(0.055kg\cdot m^2)(\alpha)$$$
$$$(4.9s^{-2})=(0.18)\alpha$$$
$$$\alpha=\frac{4.9s^{-2}}{0.18}=27.2\:s^{-2}$$$
$$$27.2\:s^{-2}$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked