Mach Number
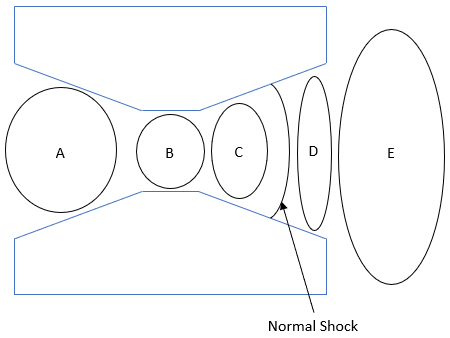
The shown figure is a cross section of a testing chamber with a converging/diverging nozzle. If a gas mixture (c = 300 m/s) experiences a normal shock wave as shown by being accelerated from 250 m/s through the chamber’s nozzle, what section is the Mach number = 1?
Expand Hint
The Mach Number is a dimensionless value useful for analyzing fluid flow dynamics problems where compressibility is a significant factor.
$$$Ma=\frac{v}{c}$$$
where
$$Ma$$
is the Mach number,
$$v$$
is the fluid flow speed, and
$$c$$
is the speed of sound.
Hint 2
In a normal shock situation, flow slows down from supersonic to subsonic, so section C has
$$Ma>1$$
and section D has
$$Ma< 1$$
.
The Mach Number is a dimensionless value useful for analyzing fluid flow dynamics problems where compressibility is a significant factor.
$$$Ma=\frac{v}{c}$$$
where
$$Ma$$
is the Mach number,
$$v$$
is the fluid flow speed, and
$$c$$
is the speed of sound (which varies based on medium conditions).
- If the Mach number is < 1 , the flow speed is lower than the speed of sound - and the speed is subsonic .
- If the Mach number is ~ 1 , the flow speed is approximately like the speed of sound - and the speed is transonic .
- If the Mach number is > 1 , the flow speed is higher than the speed of sound - and the speed is supersonic .
- If the Mach number is >> 1 , the flow speed is much higher than the speed of sound - and the speed is hypersonic .
The flow is subsonic in the chamber because
$$Ma=250/300=0.83$$
, so
$$Ma< 1$$
in section A. Flow in a converging/diverging nozzle transitioning from subsonic to supersonic will have
$$Ma=1$$
at the throat, so section B is the transonic phase. In a normal shock situation, flow slows down from supersonic to subsonic, so section C has
$$Ma>1$$
and section D
$$Ma< 1$$
. Because section E expands to an ambient environment, the flow must be subsonic.
B
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Normal Shock Relationships
570. Mach
622. Supersonic
626. Transonic
Similar Problems from FE Sub Section: Mach Number
286. Fighter Jet
564. Rocket
570. Mach
612. Speed of Sound
620. Molecular Weight
622. Supersonic
624. Atmospheric Temp
626. Transonic
Similar Problems from FE Section: Compressible Flow
286. Fighter Jet
564. Rocket
570. Mach
612. Speed of Sound
620. Molecular Weight
622. Supersonic
624. Atmospheric Temp
626. Transonic