Thermal Resistance
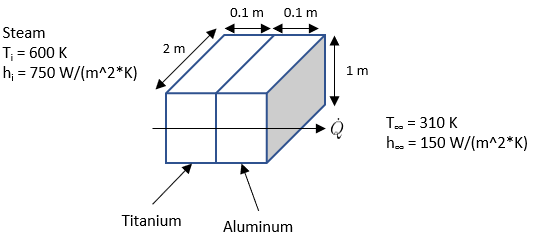
In the figure below, two metals plates are stacked side-by-side, with hot steam on one end, and ambient air on the other. If Titanium has a thermal conductivity of k = 50 W/m∙K, and Aluminum has k = 240 W/m∙K, what is the heat flux through the plate system?
Expand Hint
Thermal Resistance:
$$$\dot{Q}=\frac{\Delta T}{R_{total}}$$$
where
$$\dot Q$$
is the rate of heat transfer in Watts,
$$\Delta T$$
is the change in temperature in Kelvin, and
$$R_{total}$$
is the resistances in series.
Hint 2
Plane Wall Conduction Resistance is
$$$R=\frac{L}{kA}$$$
where
$$L$$
is the wall thickness,
$$k$$
is the thermal conductivity, and
$$A$$
is the convection surface area. For convection resistance:
$$$R=\frac{1}{hA}$$$
where
$$h$$
is the convection heat-transfer coefficient of the fluid, and
$$A$$
is the convection surface area.
Because there are two different material plates adjacent to each other, we have thermal resistances in series:
$$$\dot{Q}=\frac{\Delta T}{R_{total}}$$$
where
$$\dot Q$$
is the rate of heat transfer in Watts,
$$\Delta T$$
is the change in temperature in Kelvin, and
$$R_{total}$$
is the resistances in series. Conduction is occurring within the contacting plates, and convection is occurring between the steam/Titanium and the Aluminum/ambient environment. Resistances in series are added:
$$R_{total}=\Sigma R$$
, where Plane Wall Conduction Resistance is
$$$R=\frac{L}{kA}$$$
where
$$L$$
is the wall thickness,
$$k$$
is the thermal conductivity, and
$$A$$
is the convection surface area. For convection resistance:
$$$R=\frac{1}{hA}$$$
where
$$h$$
is the convection heat-transfer coefficient of the fluid, and
$$A$$
is the convection surface area. Thus,
$$$R_{total}=\frac{1}{A}[\frac{1}{h_i}+\frac{L_{Ti}}{k_{Ti}}+\frac{L_{Al}}{k_{Al}}+\frac{1}{h_\infty}]$$$
$$$=\frac{1}{(2m)(1m)}[\frac{1}{750W/m^2\cdot K}+\frac{0.1m}{50W/m\cdot K}+\frac{0.1m}{240W/m\cdot K}+\frac{1}{150W/m^2\cdot K}]$$$
$$$=\frac{1}{2m^2}[0.00133\frac{m^2\cdot K}{W}+0.002\frac{m^2\cdot K}{W}+0.000416\frac{m^2\cdot K}{W}+0.00667\frac{m^2\cdot K}{W}]$$$
$$$R_{total}=\frac{1}{2}[0.0104\frac{K}{W}]=0.0052\:\frac{K}{W}$$$
To find the heat rate:
$$$\dot{Q}=\frac{(T_{i}-T_{\infty })}{0.0052\frac{K}{W}}=\frac{(600K-310K)W}{0.0052K}=55,769\:W$$$
Since heat flux is
$$q_x"=\dot Q/Area$$
$$$q_x"=\frac{55,769W}{(2m)(1m)}=27,885\:\frac{W}{m^2}$$$
$$$27,885\:W/m^2$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Thermal Resistance
Similar Problems from FE Section: Conduction
227. Lumped Capacitance Model
269. Transient Conduction
400. Lumped Capacitance
634. Biot Number