Reliability Study
A reliability study was conducted for the four component system below, which has two parallel components in series with two other components. Each component was individually tested to determine the probability of it functioning properly, with the results noted in their respective boxes. What is the reliability of the entire system?
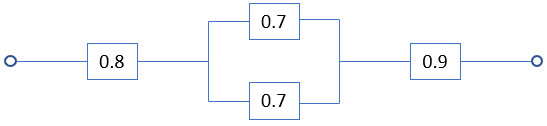
Expand Hint
For
$$n$$
components connected in series:
$$$R(P_1,P_2,...P_n)=\prod_{i=1}^{n}P_i$$$
where
$$P_i$$
is the probability that component
$$i$$
is functioning, and
$$R(P_1,P_2,...P_n)$$
is the reliability function.
Hint 2
For
$$n$$
components connected in parallel:
$$$R(P_1,P_2,...P_n)=1-\prod_{i=1}^{n}(1-P_i)$$$
where
$$P_i$$
is the probability that component
$$i$$
is functioning, and
$$R(P_1,P_2,...P_n)$$
is the reliability function.
This problem can be broken into two parts. Let’s simplify the diagram by evaluating the components in parallel. For
$$n$$
components connected in series:
$$$R(P_1,P_2,...P_n)=\prod_{i=1}^{n}P_i$$$
where
$$P_i$$
is the probability that component
$$i$$
is functioning, and
$$R(P_1,P_2,...P_n)$$
is the reliability function, which represents the system’s probability of
$$n$$
components working.
$$$R(P_1,P_2)_{parallel}=1-\prod_{i=1}^{2}(1-P_i)=1-(1-0.7)(1-0.7)$$$
Remember
$$\Pi$$
is the product notation used in math to indicate repeated multiplication. Using the FOIL method to solve the binomial:
$$$R_{parallel}=1-(1-0.7-0.7+0.49)=1-(0.09)=0.91$$$
$$R_{parallel}$$
is now in series with the first and last components.

For
$$n$$
components connected in series:
$$$R(P_1,P_2,...P_n)=\prod_{i=1}^{n}P_i$$$
where
$$P_i$$
is the probability that component
$$i$$
is functioning, and
$$R(P_1,P_2,...P_n)$$
is the reliability function, which represents the system’s probability of
$$n$$
components working.
$$$R(P_1,P_2,P_3)_{series}=\prod_{i=1}^{3}P_i=0.8\times 0.91\times0.9=0.6552$$$
Thus, the entire system’s reliability is 0.66.
0.66
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Probability
Similar Problems from FE Section: Reliability