Pressurized Pump Power
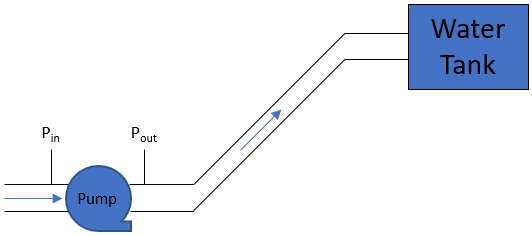
In the shown figure, a water pump with 90% efficiency is pushing fluid upward at a 5 cubic meters per second flow rate. If the measured inlet and outlet pressures are measured at 500 kPa and 150 kPa respectively, what is the minimum pump power required in kW? Assume the specific weight of water is 9.8 kN/m^3.
Expand Hint
The pump power equation:
$$$\dot{W}=\frac{Q\gamma h}{\eta_t}$$$
where
$$Q$$
is the volumetric flow,
$$h$$
is the fluid head needed to be lifted,
$$\eta_t$$
is the total efficiency (
$$\eta_{pump} \times \eta_{motor}$$
),
$$\dot W$$
is the power, and
$$\gamma$$
is the specific weight of the fluid.
Hint 2
How pressure changes with elevation in a fluid can be expressed as:
$$$\Delta P=\gamma \times \Delta h$$$
where
$$\Delta P$$
is the change is pressure,
$$\Delta h$$
is the change in height, and
$$\gamma $$
is the fluid’s specific weight (
$$density \times gravity$$
).
The pump power equation:
$$$\dot{W}=\frac{Q\gamma h}{\eta_t}$$$
where
$$Q$$
is the volumetric flow,
$$h$$
is the fluid head needed to be lifted,
$$\eta_t$$
is the total efficiency (
$$\eta_{pump} \times \eta_{motor}$$
),
$$\dot W$$
is the power, and
$$\gamma$$
is the specific weight of the fluid. Remember, how pressure changes with elevation in a fluid can be expressed as:
$$$\Delta P=\gamma \times \Delta h$$$
where
$$\Delta P$$
is the change is pressure,
$$\Delta h$$
is the change in height, and
$$\gamma $$
is the fluid’s specific weight (
$$density \times gravity$$
). Solving for fluid head:
$$$\Delta h=\frac{\Delta P}{\gamma}=\frac{500kPa-150kPa}{9.8kN/m^3}=\frac{350,000N/m^2}{9,800N/m^3}=35.7\:m$$$
Therefore,
$$$\dot{W}=\frac{(5m^3)(9.8kN)(35.7m)}{(sec)(m^3)(0.9)}=\frac{1,749.3kN\cdot m}{0.9(sec)}=1,944\:kW$$$
1,944 kW
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Pump Power Equation
182. Pump Power
213. Centrifugal Fan
323. Pump Work
366. Pump Efficiency
514. A Pump’s Efficiency
601. A Pump’s Pressure
Similar Problems from FE Sub Section: The Pressure Field in a Static Liquid
014. Swimming Pool Pressure
311. Water Tower
351. Absolute vs Gauge Pressure
352. Pressure Difference
578. Water Height
601. A Pump’s Pressure
Similar Problems from FE Section: Fluid Flow Machinery
182. Pump Power
199. Affinity Law
213. Centrifugal Fan
323. Pump Work
348. Centrifugal Pump
366. Pump Efficiency
474. Affinity
477. Scaling Law
514. A Pump’s Efficiency
539. Impeller Diameter
601. A Pump’s Pressure
Similar Problems from FE Section: Characteristics of a Static Liquid
014. Swimming Pool Pressure
033. Archimedes' Principle
311. Water Tower
351. Absolute vs Gauge Pressure
352. Pressure Difference
578. Water Height
601. A Pump’s Pressure