Water Tower
Consider a small city’s water tower has its storage tank open to the atmosphere with an attached 1 m^2 diameter connector pipe. What is the gauge pressure (kPa) at the outlet if the exit valve is closed? Assume the pipe and tank are completely full of water.
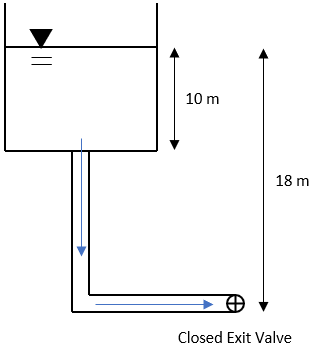
Expand Hint
Note the density of water is
$$1,000\:kg/m^3$$
.
Hint 2
The pressure field in a static liquid:
$$$P=\rho gh=\gamma h$$$
where
$$\rho$$
is the density,
$$g$$
is the acceleration due to gravity,
$$h$$
is the height, and
$$\gamma$$
is the fluid’s specific weight.
The pressure field in a static liquid:
$$$P=\rho gh=\gamma h$$$
where
$$\rho$$
is the density,
$$g$$
is the acceleration due to gravity,
$$h$$
is the height, and
$$\gamma$$
is the fluid’s specific weight. Since the density of water is
$$1,000\:kg/m^3$$
:
$$$P=(1,000\frac{kg}{m^3})(9.8\frac{m}{s^2})(18m)=176,400\frac{kg}{m\cdot s^2}=176.4\:kPa$$$
An alternative way to solve for pressure is by using the specific weight of water:
$$$P=(9,800\frac{kg}{m^2\cdot s^2})(18m)=176,400\frac{kg}{m\cdot s^2}=176.4\:kPa$$$
176.4 kPa
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: The Pressure Field in a Static Liquid
014. Swimming Pool Pressure
297. Pressurized Pump Power
351. Absolute vs Gauge Pressure
352. Pressure Difference
578. Water Height
601. A Pump’s Pressure
Similar Problems from FE Section: Characteristics of a Static Liquid
014. Swimming Pool Pressure
033. Archimedes' Principle
297. Pressurized Pump Power
351. Absolute vs Gauge Pressure
352. Pressure Difference
578. Water Height
601. A Pump’s Pressure