Centrifugal Pump
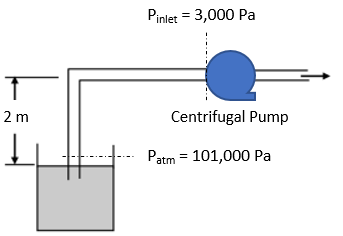
Consider a centrifugal pump is used to pull water from a large storage reservoir exposed to the atmosphere at sea level. The water flows at a constant rate of 0.10 m^3/min through a 1.25 cm diameter pipe with a friction coefficient of 0.5. The pump is placed 2.0 m above the reservoir’s water level and the vapor pressure at the pump’s inlet is noted to be 3,000 Pa. Will the pump operate properly if the manufacturer recommends a net positive suction head (NPSH) of at least 1.25? Assume turbulent flow and note the density of water to be 1,000 kg/m^3.
Expand Hint
Cavitation damages a pump’s propeller, and is caused by liquid turning into a vapor through pressure decreases instead of typical heating methods (i.e. boiling). As pockets of water vapor travel to areas of greater pressure, the region of low pressure can collapse suddenly, creating concentrated shockwaves that can cause structural damage. Net Positive Suction Head Required (
$$NPSH_R)$$
, a property of the pump, is the amount of net positive suction head needed to avoid cavitation. Net Positive Suction Head Available (
$$NPSH_A)$$
, a pipe system property, is the amount of net positive suction head it can provide to the pump. To prevent cavitation:
$$$NPSH_A> NPSH_R$$$
Hint 2
Net Positive Suction Head Available (
$$NPSH_A$$
):
$$$NPSH_A=H_{pa}+H_s-\sum h_L-H_{vp}=\frac{P_{inlet}}{\rho g}+\frac{v_{inlet}^2}{2g}-\frac{P_{vapor}}{\rho g}$$$
where
$$H_{pa}$$
is the atmospheric pressure head on the liquid’s surface in the sump,
$$H_s$$
is the liquid’s static suction head (liquid surface height above the pump impeller centerline),
$$\sum h_L$$
is the total friction loss in the suction line,
$$H_{vp}$$
is the liquid’s vapor pressure head at the operating temperature,
$$v$$
is the fluid velocity at the pump inlet,
$$P_{vapor}$$
is the fluid vapor pressure at pump inlet,
$$\rho$$
is the fluid density, and
$$g$$
is the acceleration due to gravity.
Cavitation damages a pump’s propeller, and is caused by liquid turning into a vapor through pressure decreases instead of typical heating methods (i.e. boiling). As pockets of water vapor travel to areas of greater pressure, the region of low pressure can collapse suddenly, creating concentrated shockwaves that can cause structural damage. Net Positive Suction Head Required (
$$NPSH_R)$$
, a property of the pump, is the amount of net positive suction head needed to avoid cavitation. Net Positive Suction Head Available (
$$NPSH_A)$$
, a pipe system property, is the amount of net positive suction head it can provide to the pump. To prevent cavitation:
$$$NPSH_A> NPSH_R$$$
Net Positive Suction Head Available (
$$NPSH_A$$
) has a general formula of:
$$$NPSH_A=H_{pa}+H_s-\sum h_L-H_{vp}=\frac{P_{inlet}}{\rho g}+\frac{v_{inlet}^2}{2g}-\frac{P_{vapor}}{\rho g}$$$
where
$$H_{pa}$$
is the atmospheric pressure head on the liquid’s surface in the sump,
$$H_s$$
is the liquid’s static suction head (liquid surface height above the pump impeller centerline),
$$\sum h_L$$
is the total friction loss in the suction line,
$$H_{vp}$$
is the liquid’s vapor pressure head at the operating temperature,
$$v$$
is the fluid velocity at the pump inlet,
$$P_{vapor}$$
is the fluid vapor pressure at pump inlet,
$$\rho$$
is the fluid density, and
$$g$$
is the acceleration due to gravity.
Setting point 1 to be on the tank’s surface and point 2 upstream at the pump’s entrance, we can apply the extended Bernoulli Equation from points 1 to 2:
$$$(\frac{P}{\rho g}+\frac{v^2}{2g}+z)_2=(\frac{P}{\rho g}+\frac{v^2}{2g}+z)_1-h_{L,12}$$$
Based on the problem statement givens:
$$$P_{1}=P_{atm}=101,000\:Pa$$$
$$$P_2=P_{inlet}$$$
$$v_1=0$$
because it’s a big tank so water level drop is negligible.
$$v_2=v_{inlet}$$
(we’ll need to convert volumetric flow rate later).
$$$z_2-z_1=2\:m=H_s$$$
$$h_{L,12}=?$$
(needs to be calculated later)
Rearranging the extended Bernoulli equation between points 1 and 2 to match the form of the NPSH equation:
$$$\frac{P_{inlet}}{\rho g}+\frac{v_{inlet}^2}{2g}=\frac{P_{atm}}{\rho g}+z_1-z_2-h_{L,12}$$$
Subtracting
$$P_{vapor}$$
from both sides of the equation:
$$$\frac{P_{inlet}}{\rho g}+\frac{v_{inlet}^2}{2g}-\frac{P_{vapor}}{\rho g}=\frac{P_{atm}}{\rho g}-\frac{P_{vapor}}{\rho g}-H_s-h_{L,12}=NPSH_A$$$
We now know everything but the head loss in the pipe. First, let’s convert the volumetric flow rate into velocity by dividing by the pipe’s area:
$$$v=\frac{\dot{Q}}{area}=\frac{0.10\frac{m^3}{min}\cdot \frac{1min}{60sec}}{\frac{\pi}{4}(0.0125m)^2}=\frac{0.001667m^3}{(sec)\frac{\pi}{4}(0.00015625m^2)}$$$
$$$v=\frac{0.001667}{0.00012265}\frac{m}{s}=13.6\:m/s$$$
Remember, a pipe’s head loss is
$$$h_L=\frac{C_fu^2}{2g}$$$
where
$$C_f$$
is the friction coefficient,
$$u$$
is the fluid velocity, and
$$g$$
is the acceleration due to gravity.
$$$h_L=\frac{(0.5)(13.6m/s)^2}{2(9.8m/s^2)}=\frac{(0.5)(184.96m^2/s^2)}{19.6m/s^2}=4.7\:m$$$
Therefore, we can solve for the Net Positive Suction Head Available:
$$$NPSH_A=\frac{101,000Pa}{1,000kg/m^3 (9.8m/s^2)}-\frac{3,000Pa}{1,000kg/m^3 (9.8m/s^2)}-2m-4.7m$$$
$$$=\frac{101,000N}{9,800kg/s^2}-\frac{3,000N}{9,800kg/s^2}-6.7m$$$
$$$=\frac{101,000kg\cdot m}{(s^2)9,800kg/s^2}-\frac{3,000kg\cdot m}{(s^2)9,800kg/s^2}-6.7m$$$
$$$NPSH_A=10.306m-0.306m-6.7=3.3\:m $$$
Because the problem statement says the manufacturer’s
$$NPSH_R$$
rating is 1.25:
$$$NPSH_A> NPSH_R$$$
Thus, the pump will function properly.
The pump will function properly.
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Centrifugal Pump Characteristics
Similar Problems from FE Sub Section: Bernoulli Equation
Similar Problems from FE Section: Fluid Flow Machinery
182. Pump Power
199. Affinity Law
213. Centrifugal Fan
297. Pressurized Pump Power
323. Pump Work
366. Pump Efficiency
474. Affinity
477. Scaling Law
514. A Pump’s Efficiency
539. Impeller Diameter
601. A Pump’s Pressure
Similar Problems from FE Section: Principles of One-Dimensional Fluid Flow
178. Fluid Velocity
248. Fluid Flow
366. Pump Efficiency
554. Fluid Density