Pressure Difference
At 10,994 meters below sea level, the Mariana Trench is the deepest known point in the Earth’s ocean. If a submarine is exploring the ocean depths 2,500 m above the Trench’s floor, what is the difference in pressure between the submarine and sea level? Assume the density of salt water is 1,026 kg/m^3 and is constant throughout the ocean’s depths.
Expand Hint
The pressure difference between two different points:
$$$P_2-P_1=-\gamma(z_2-z_1)=-\gamma h=-\rho gh$$$
where
$$\gamma $$
is the liquid’s specific weight,
$$\rho$$
is the liquid’s density, and
$$g$$
is the acceleration due to gravity
Hint 2
$$P_2$$
,
$$P_1$$
,
$$z_1$$
,
$$z_2$$
, and
$$h$$
are defined as:
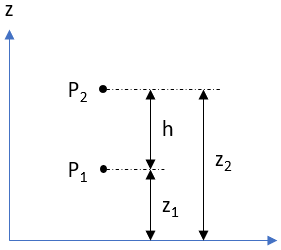
The pressure difference between two different points:
$$$P_2-P_1=-\gamma(z_2-z_1)=-\gamma h=-\rho gh$$$
where
$$\gamma $$
is the liquid’s specific weight,
$$\rho$$
is the liquid’s density,
$$g$$
is the acceleration due to gravity, and
$$P_2$$
,
$$P_1$$
,
$$z_1$$
,
$$z_2$$
, and
$$h$$
are defined as:
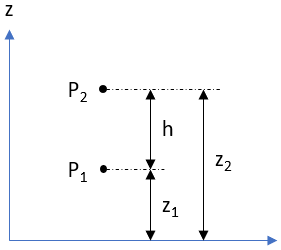
Based on the problem statement, the submarine is at
$$P_1$$
and sea level is at
$$P_2$$
. It also gives
$$z_1$$
and
$$z_2$$
for the fact about the Mariana Trench’s depth and the submarine’s location. Thus,
$$$P_2-P_1=\rho gh=\rho g(z_2-z_1)=(1,026\frac{kg}{m^3})(9.8\frac{m}{s^2})(10,994m-2,500m)$$$
$$$\Delta P=10,054.8\frac{N}{m^3}(8,494m)=85,405,471\frac{N}{m^2}=85\:MPa$$$
85 MPa
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: The Pressure Field in a Static Liquid
014. Swimming Pool Pressure
297. Pressurized Pump Power
311. Water Tower
351. Absolute vs Gauge Pressure
578. Water Height
601. A Pump’s Pressure
Similar Problems from FE Section: Characteristics of a Static Liquid
014. Swimming Pool Pressure
033. Archimedes' Principle
297. Pressurized Pump Power
311. Water Tower
351. Absolute vs Gauge Pressure
578. Water Height
601. A Pump’s Pressure