Confidence Interval
To test for yield strength, consider 40 aluminum test specimens were subjected to a tensile load test. If the standard deviation is 2.5 and the sample mean is 200 MPa, what is the 95% confidence interval for the aluminum’s yield strength?
Expand Hint
The population’s standard deviation,
$$\sigma$$
, is known, and the sample size is greater than 30. Thus, let’s use the z distribution. Only use the t distribution if
$$\sigma$$
is unknown and if the sample size is less than 30.
Hint 2
The Confidence Interval for the Mean µ of a Normal Distribution when a standard deviation
$$\sigma$$
is known:
$$$\bar{X}-Z_{a/2}\frac{\sigma}{\sqrt{n}}\leq \mu \leq \bar{X}+Z_{a/2}\frac{\sigma}{\sqrt{n}}$$$
where
$$\bar{X}$$
is the sample mean,
$$\sigma$$
is the standard deviation,
$$n$$
is the sample size, and
$$Z_a$$
corresponds to the appropriate probability under the normal probability curve for a given
$$Z_{var}$$
(standard normal Z score).
The population’s standard deviation,
$$\sigma$$
, is known, and the sample size is greater than 30. Thus, let’s use the z distribution. Only use the t distribution if
$$\sigma$$
is unknown and if the sample size is less than 30.
The Confidence Interval for the Mean µ of a Normal Distribution when a standard deviation
$$\sigma$$
is known:
$$$\bar{X}-Z_{a/2}\frac{\sigma}{\sqrt{n}}\leq \mu \leq \bar{X}+Z_{a/2}\frac{\sigma}{\sqrt{n}}$$$
where
$$\bar{X}$$
is the sample mean,
$$\sigma$$
is the standard deviation,
$$n$$
is the sample size, and
$$Z_a$$
corresponds to the appropriate probability under the normal probability curve for a given
$$Z_{var}$$
(standard normal Z score).
$$Z_{a/2}$$
is usually derived from confidence interval table (like in the FE exam handbook):
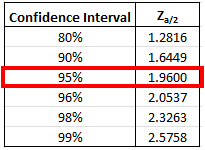
Therefore, the 95% confidence interval is:
$$$200-1.96\frac{2.5}{\sqrt{40}}\leq \mu \leq 200+1.96\frac{2.5}{\sqrt{40}}$$$
$$$200-1.96(0.395)\leq \mu \leq 200+1.96(0.395)$$$
$$$200-0.775\leq \mu \leq 200+0.775$$$
$$$199.22\leq \mu \leq 200.78$$$
Thus, the answer is (199.22, 200.78).
(199.22, 200.78)
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Confidence Interval for the Mean µ of a Normal Distribution
587. Interval of Confidence
Similar Problems from FE Sub Section: Values of Z
587. Interval of Confidence
Similar Problems from FE Section: Confidence Intervals, Sample Distributions and Sample Size
587. Interval of Confidence
Similar Problems from FE Section: Test Statistics
587. Interval of Confidence