Superposition
The cantilevered beam shown has a modulus of elasticity of 70 GPa and a moment of inertia of 0.0001 m^4. What is the beam’s deflection at mid-span?
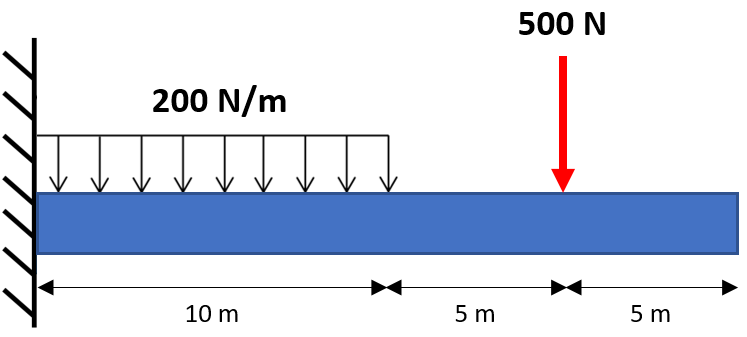
Expand Hint
Superposition:

Hint 2
The final answer should be negative to indicate a downward deflection.
The figure can be broken down into two easier problems via superposition:

Referencing the cantilevered beam slopes and deflections section in the FE handbook (or any other ref table), the deflection formula for a partial distributed load that represents our sub-figure is:
$$$v=\frac{-wx^2}{24EI}(x^2-2Lx+\frac{3}{2}L^2)$$$
where
$$w$$
is the distributed load,
$$x$$
is the designated deflection point of interest (
$$0\leq x\leq L/2$$
),
$$L$$
is the beam’s length,
$$E$$
is the modulus of elasticity, and
$$I$$
is the moment of inertia. Note, this equation is only valid when the designated deflection point of interest from the fixed end is less than or equal to the 1/2 of the beam’s length from the fixed end.
Because the problem is asking for the deflection at the mid-span,
$$x=10$$
:
$$$v=\frac{-(200N)(10m)^2(m^2)}{(m)24(70\cdot 10^9N)(0.0001m^4)}((10m)^2-2(20m)(10m)+\frac{3}{2}(20m)^2)$$$
$$$=\frac{-20,000}{(m)0.0024(70\cdot 10^9)}(100m^2-400m^2+600m^2)$$$
$$$=\frac{-20,000}{0.168\cdot 10^9}(300m)=-0.0357\:m$$$
Referencing the cantilevered beam slopes and deflections section in the FE handbook (or any other ref table), the deflection formula for a point load that represents our partial figure is:
$$$v=\frac{-Px^2}{6EI}(-x+3a)$$$
where
$$P$$
is the point load,
$$x$$
is the designated deflection point of interest,
$$a$$
is the point load’s distance from the beam’s fixed end,
$$E$$
is the modulus of elasticity, and
$$I$$
is the moment of inertia. Note, this equation is only valid when the designated deflection point of interest from the fixed end is less than the point load’s distance from the fixed end.
Because the problem is asking for the deflection at the mid-span,
$$x=10$$
:
$$$v=\frac{-(500N)(10m)^2}{6(70\cdot 10^9Pa)(0.0001m^4)}(-(10m)+3(15m))$$$
$$$=\frac{-(500N)(100m^2)(m^2)}{(420\cdot 10^9N)(0.0001m^4)}(-10m+45m)=\frac{-50,000}{4.2\cdot 10^7}(35m)$$$
$$$=(-0.00119)(35m)=-0.042\:m$$$
Adding the two deflections to get the beam’s deflection at the mid-point:
$$$-0.042m+-0.0357m=-0.078\:m$$$
-0.078 m
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Cantilevered Beam Slopes and Deflections
168. Cantilevered Beam
267. Vertically Cantilevered
Similar Problems from FE Section: Material Properties
168. Cantilevered Beam
267. Vertically Cantilevered