Angle of Refraction
A child underwater in a pool shines a flashlight towards the surface at a 40° angle from the vertical. What angle does the beam of light leave the pool? Note the index of refraction for water and air are 1.33 and 1.00 respectively.
Expand Hint
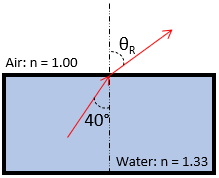
Hint 2
Snell’s Law:
$$$n_isin\theta_i=n_rsin\theta_r$$$
where
$$n_i$$
is the incident index,
$$n_r$$
is the refracted index,
$$\theta_i$$
is the incident angle, and
$$\theta_r$$
is the refracted angle.
Snell’s Law:
$$$n_isin\theta_i=n_rsin\theta_r$$$
where
$$n_i$$
is the incident index,
$$n_r$$
is the refracted index,
$$\theta_i$$
is the incident angle, and
$$\theta_r$$
is the refracted angle.
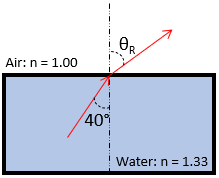
Thus, the refracted angle is:
$$$(1.33)sin40^{\circ}=(1.00)sin\theta_r$$$
$$$sin\theta_r=\frac{0.855}{1.00}=0.855$$$
$$$\theta_r=sin^{-1}(0.855)=58.7^{\circ}$$$
58.7°
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked