Pulley + Belt
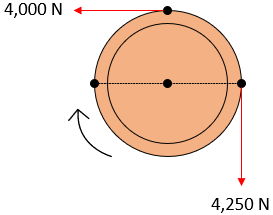
In the figure shown, a pulley is driven by a belt. What minimum coefficient of friction will prevent slipping between pulley and belt? Ignore centrifugal effects.
Expand Hint
Belt Friction:
$$$F_1=F_2e^{\mu \theta}$$$
where
$$F_1$$
is the applied force in the direction of impending motion,
$$F_2$$
is the applied force resisting impending motion,
$$\mu$$
is the static coefficient of friction, and
$$\theta$$
is the total angle of contact between surfaces in radians.
Hint 2
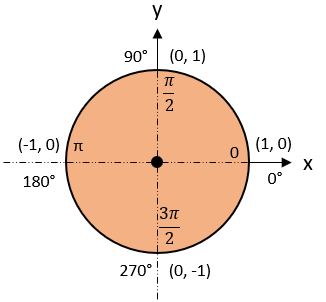
Unit Circle:
Belt Friction:
$$$F_1=F_2e^{\mu \theta}$$$
where
$$F_1$$
is the applied force in the direction of impending motion,
$$F_2$$
is the applied force resisting impending motion,
$$\mu$$
is the static coefficient of friction, and
$$\theta$$
is the total angle of contact between surfaces in radians. Recall a unit circle to determine
$$\theta$$
:
Therefore,
$$$4,250N=(4,000N)e^{\mu \pi/2}$$$
Solving for the coefficient of friction:
$$$ln(\frac{4,250}{4,000})=ln(e^{\mu \pi/2})=\mu \frac{\pi }{2}$$$
$$$\mu=\frac{2}{\pi}\cdot ln(\frac{4,250}{4,000})=\frac{2}{\pi} \cdot 0.06=0.04$$$
0.04
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Section: Belt Friction
382. Belt Friction
406. Pulley & Belt
579. Belt Force
584. Belt