Chrome Silicon Wire
A chrome silicon wire with a diameter of 10 cm will be used as a spring material in a static assembly. Approximate the max allowable torsional stress for the wire.
Expand Hint
The max allowable torsional stress for hardened and tempered carbon and low-alloy steels in static applications can be approximated as:
$$$S_{sy}=\tau = 0.50\times S_{ut}$$$
Hint 2
For spring materials, the minimum tensile strength for common spring steels can be determined from:
$$$S_{ut}=\frac{A}{d^{m}}$$$
where
$$S_{ut}$$
is the tensile strength in MPa, and
$$d$$
is the wire diameter in millimeters.
The max allowable torsional stress for hardened and tempered carbon and low-alloy steels (ASTM A232 & A401) in static applications can be approximated as:
$$$S_{sy}=\tau = 0.50\times S_{ut}$$$
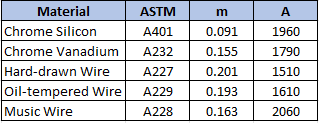
For spring materials, the minimum tensile strength for common spring steels can be determined from:
$$$S_{ut}=\frac{A}{d^{m}}$$$
where
$$S_{ut}$$
is the tensile strength in MPa,
$$d$$
is the wire diameter in millimeters, and
$$A$$
and
$$m$$
can be found in the shown table:
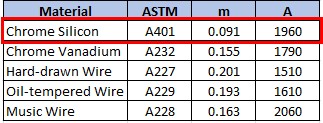
Since the problem is asking for a chrome silicon wire:
$$$S_{ut}=\frac{1960}{(100mm)^{0.091}}=\frac{1960}{1.521}=1,289\: MPa$$$
Thus, the max allowable torsional stress for a chrome silicon wire is approximately:
$$$\tau = 0.50\times (1,289MPa)=645\:MPa$$$
645 MPa
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Springs
135. Helical Spring
141. Tensile Strength for Springs
205. Compression Spring
206. Spring Force
265. Mechanical Springs
335. Spring Stretch
339. Compressing a Spring
341. Parallel Springs
343. Springs in Series
371. Spring Compression
381. Series of Springs
384. Springs in Parallel
386. Compounding Springs
387. Spring Tensile Strength
388. Torsional Stress
456. Free Length Spring
478. Spring Stretching
484. Correction Factor
486. Bending Stress
574. Spring Load
575. ASTM 232
576. Applied Force
Similar Problems from FE Section: Mechanical Design and Analysis
135. Helical Spring
141. Tensile Strength for Springs
205. Compression Spring
206. Spring Force
265. Mechanical Springs
280. Joint Shear Stress
295. Planetary Gear
296. Roller Bearing
299. Ball Bearing
335. Spring Stretch
337. Power Screw
339. Compressing a Spring
341. Parallel Springs
343. Springs in Series
347. Bolt Diameter
371. Spring Compression
381. Series of Springs
384. Springs in Parallel
386. Compounding Springs
387. Spring Tensile Strength
388. Torsional Stress
456. Free Length Spring
458. Rivet Strength
478. Spring Stretching
480. Threaded Fastener Load
481. Max Tension Load
483. Fatigue Loading
484. Correction Factor
485. Mean Stress
486. Bending Stress
516. Power Screw Torque
520. Power Screw Load
540. Bearing
547. Power Screw Lead
565. Design Life
574. Spring Load
575. ASTM 232
576. Applied Force
577. Preload
589. Threaded Load
590. Minimum Tensile
591. Joint Coefficient
594. Threaded Preload
596. Tensile Area
603. Bearing Type
630. Type of Bearing