Dot Prod
What is the dot product of [V•W]?
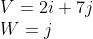
Expand Hint
The dot product, or scalar product, is an mathematical operation that takes two vectors and returns a single number. It is the projection of vector B onto vector A multiplied by the determinant of vector A.
Hint 2
The dot product of vectors A and B:
$$$A\cdot B=a_xb_x+a_yb_y+a_zb_z=|A||B|cos\theta =B\cdot A$$$
where
$$A=a_x\textbf{i}+a_y\textbf{j}+a_z\textbf{k}$$
,
$$B=b_x\textbf{i}+b_y\textbf{j}+b_z\textbf{k}$$
,
$$|A|$$
is the determinant of vector A, and
$$|B|$$
is the determinant of vector B.
The dot product, or scalar product, is an mathematical operation that takes two vectors and returns a single number. It is the projection of vector B onto vector A multiplied by the determinant of vector A. The dot product of vectors A and B:
$$$A\cdot B=a_xb_x+a_yb_y+a_zb_z=|A||B|cos\theta =B\cdot A$$$
where
$$|A|$$
is the determinant of vector A,
$$|B|$$
is the determinant of vector B, and:
$$A=a_x\textbf{i}+a_y\textbf{j}+a_z\textbf{k}$$
$$B=b_x\textbf{i}+b_y\textbf{j}+b_z\textbf{k}$$
Remember, vector W can be written as
$$W=0i+1j$$
. Thus,
$$$V\cdot W=v_xw_x+v_yw_y=(2)(0)+(7)(1)=0+7=7$$$
7
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Vectors
049. Cross Products
050. Unit Vectors
306. Dot Product
424. Vector Dot Product
535. X Product
543. Cross vs Dot Product
546. Vector Unit
639. Vector Combinations
Similar Problems from FE Section: Determinants
049. Cross Products
050. Unit Vectors
123. Matrix Determinant
251. Matrix
252. Larger Determinant
256. 4x4 Matrix
306. Dot Product
424. Vector Dot Product
447. 3x3 Matrix
503. Determinant Matrix
504. 3x3 Determinant
535. X Product
543. Cross vs Dot Product
546. Vector Unit
633. 2x2 Matrix
639. Vector Combinations