Ramp Sliding
Consider a current equilibrium state where a 10 kg box is on an inclined ramp. The coefficient of static friction between the two is 0.75. As the ramp is pivoted upwards, what angle (degrees) will the box begin to slide? If the box weighed 1.5x as much, what angle (degrees) would it begin to slide?

Expand Hint
Free Body Diagram:
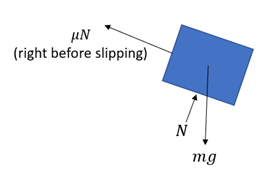
Hint 2
Analyzing the forces normal to the ramp:
$$$\sum F_{normal}=0=N-(mass\times gravity)cos\theta \rightarrow N=(mg)cos\theta $$$
First, draw the free body diagram on the box.

Analyzing the forces normal to the ramp:
$$$\sum F_{normal}=0=N-(mass\times gravity)cos\theta \rightarrow N=(mg)cos\theta $$$
Analyzing the forces tangent to the ramp:
$$$\sum F_{tangent}=0=\mu N-(mass\times gravity)sin\theta\to N=\frac{(mg)sin\theta}{\mu}$$$
Combining the two equations:
$$$\mu (mg)cos\theta =(mg)sin\theta$$$
$$$\mu=\frac{sin\theta }{cos\theta }=tan\theta =0.75$$$
$$$\theta =tan^{-1}(0.75)=36.9^{\circ}$$$
Notice how the mass does not determine the sliding angle since the x-component and y-component cancel each other out. Therefore, the box will still start sliding at 36.9°, even if it weighed 1.5x more.
- 36.9°
- 36.9°
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Friction
031. Friction on a Ramp
222. Sliding Down a Ramp
Similar Problems from FE Section: Friction
031. Friction on a Ramp
222. Sliding Down a Ramp
Similar Problems from FE Section: Impulse and Momentum
031. Friction on a Ramp
222. Sliding Down a Ramp