3x3 Determinant
Find the determinant of the shown 3 x 3 matrix:
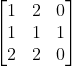
Expand Hint
$$$\begin{bmatrix}a & b & c\\ d & e & f\\ g & h & i\end{bmatrix}=a\cdot\begin{vmatrix}e & f\\ h & i\end{vmatrix}-b\cdot \begin{vmatrix}d & f\\ g & i\end{vmatrix}+c\cdot \begin{vmatrix}d & e\\ g & h\end{vmatrix}$$$
Hint 2
$$$\begin{bmatrix}a & b & c\\ d & e & f\\ g & h & i\end{bmatrix}=a(ei-fh)-b(di-fg)+c(dh-eg)$$$
For a third-order determinant:
$$$\begin{bmatrix}a & b & c\\ d & e & f\\ g & h & i\end{bmatrix}=a\cdot\begin{vmatrix}e & f\\ h & i\end{vmatrix}-b\cdot \begin{vmatrix}d & f\\ g & i\end{vmatrix}+c\cdot \begin{vmatrix}d & e\\ g & h\end{vmatrix}$$$
$$$\begin{bmatrix}a & b & c\\ d & e & f\\ g & h & i\end{bmatrix}=a(ei-fh)-b(di-fg)+c(dh-eg)$$$
Thus,
$$$\begin{bmatrix}1 & 2 & 0\\ 1 & 1 & 1\\ 2 & 2 & 0\end{bmatrix}=1[(1)(0)-(1)(2)]-2[(1)(0)-(1)(2)]+0[(1)(2)-(1)(2)]$$$
$$$=1[0-2]-2[0-2]+0$$$
$$$=1(-2)-2(-2)+0=-2+4=2$$$
2
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Third-Order Determinant
252. Larger Determinant
256. 4x4 Matrix
447. 3x3 Matrix
Similar Problems from FE Section: Determinants
049. Cross Products
050. Unit Vectors
123. Matrix Determinant
251. Matrix
252. Larger Determinant
256. 4x4 Matrix
306. Dot Product
419. Dot Prod
424. Vector Dot Product
447. 3x3 Matrix
503. Determinant Matrix
535. X Product
543. Cross vs Dot Product
546. Vector Unit
633. 2x2 Matrix
639. Vector Combinations