Product Binomial
In polar form, what is the product of the following two binomials?
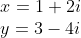
Expand Hint
Use the FOIL (
F
irst,
O
uter,
I
nner,
L
ast) method to multiply the two binomials (an expression with two terms). Remember to track +/- signs.
$$$(a+b)(c+d)=ac+ad+bc+bd$$$
Hint 2
Polar form is:
$$$z=c\: \angle \: \theta $$$
where
$$c=\sqrt{a^2+b^2}$$
(the vector’s length) and
$$\theta=tan^{-1}(b/a)$$
. Note
$$a$$
is the real component and
$$b$$
is the imaginary component of the rectangular form.
Use the FOIL (
F
irst,
O
uter,
I
nner,
L
ast) method to multiply the two binomials (an expression with two terms). Remember to track +/- signs.
$$$(a+b)(c+d)=ac+ad+bc+bd$$$
Thus,
$$$(1+2i)(3-4i)=3-4i+6i-8i^2$$$
Remember
$$i=\sqrt{-1}$$
:
$$$=3+2i-8(-1)=11+2i$$$
Complex numbers can be written in both rectangular and polar form. For rectangular form, a complex number is represented by both its real and imaginary components:
$$$z=a+jb$$$
where
$$a$$
is the real component,
$$b$$
is the imaginary component, and
$$j=\sqrt{-1}$$
which is often expressed as
$$i=\sqrt{-1}$$
.
Analyzing the rectangular coordinate form
$$11+2i$$
, let’s assign
$$a=11$$
and
$$b=2$$
.
Polar form is:
$$$z=c\: \angle \: \theta $$$
where
$$c=\sqrt{a^2+b^2}$$
(the vector’s length) and
$$\theta=tan^{-1}(b/a)$$
. Note:
$$a=c\:cos(\theta)$$
and
$$b=c\:sin(\theta)$$
.
Therefore,
$$$c=\sqrt{11^2+2^2}=\sqrt{121+4}=11.18$$$
$$$\theta=tan^{-1}(\frac{2}{11})=10.3^{\circ}$$$
Finally, the polar form is:
$$$11.18 \: \angle \: 10.3^{\circ}$$$
$$$11.18 \: \angle \: 10.3^{\circ}$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Polar Form
344. Polar Form
345. Binomial Product
552. Polar
611. The Polar Form
Similar Problems from FE Section: Algebra of Complex Numbers
344. Polar Form
345. Binomial Product
552. Polar
611. The Polar Form