Z Score
Suppose a group of people are running a marathon. Their recorded times from start to completion form a normal distribution with a mean of 3.5 hours and a standard deviation of 30 minutes. What is the probability that a runner (selected at random) takes less than 4 hours to finish the marathon? Refer to the shown Unit Normal Distribution table.
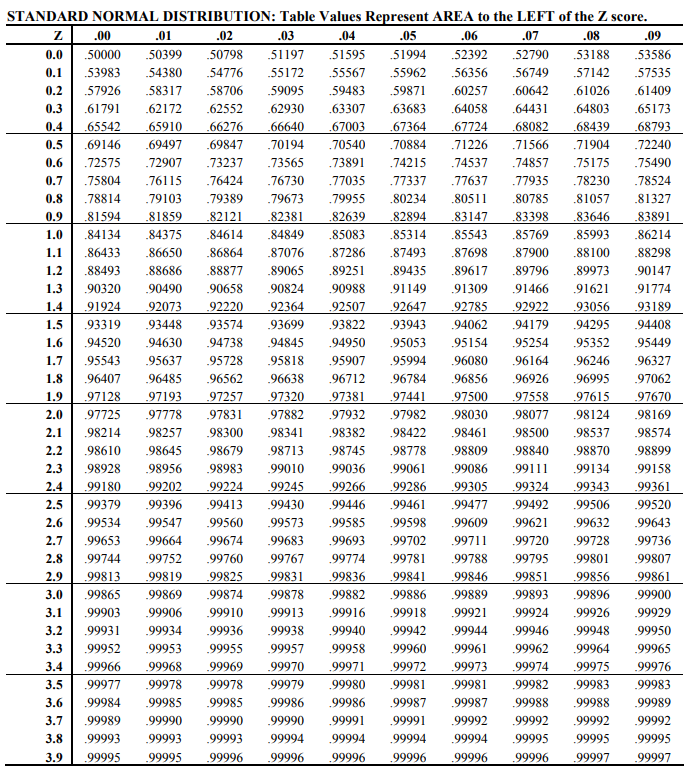
Expand Hint
For any normal distribution, the table for the unit normal distribution can be utilized via the following transformation:
$$$z=\frac{x-\mu }{\sigma }$$$
where
$$z$$
is the “Z” score associated with the unit normal distribution table,
$$\mu$$
is the mean,
$$\sigma$$
is the standard deviation, and
$$x$$
is the desired region under the bell curve.
Hint 2
$$$z=\frac{x-\mu }{\sigma }=\frac{4-3.5}{0.5}=1.00$$$
For any normal distribution, the table for the unit normal distribution can be utilized via the following transformation:
$$$z=\frac{x-\mu }{\sigma }$$$
where
$$z$$
is the “Z” score associated with the unit normal distribution table,
$$\mu$$
is the mean,
$$\sigma$$
is the standard deviation, and
$$x$$
is the desired region under the bell curve.
$$$z=\frac{x-\mu }{\sigma }=\frac{4-3.5}{0.5}=1.00$$$
Referring to the Unit Normal Distribution Table:
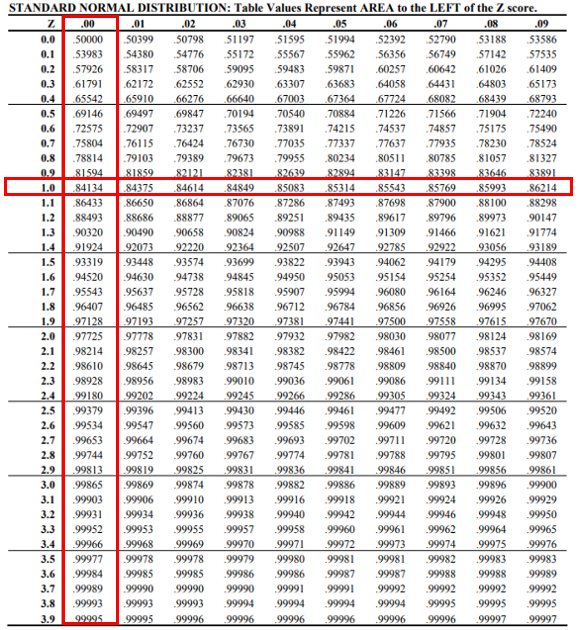
Because the label for rows contains the integer part and the first decimal place of Z, and the label for columns contains the second decimal place of Z, “.84134” is the corresponding distribution for
$$Z=1.00$$
. This represents the probability of selecting a runner whose marathon completion time is under 4 hours.
.84134
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Normal Distribution (Gaussian Distribution)
114. Obstacle Course
649. Unit Normal Distribution
Similar Problems from FE Section: Probability Functions, Distributions, and Expected Values
114. Obstacle Course
649. Unit Normal Distribution