Unit Normal Distribution
Consider a tech company with a fruit logo designs a computer circuit where the signal wavelengths form a normal distribution with a standard deviation of 1.25 and a mean of 5. If a random signal is selected, what is the probability its wavelength will be more than 6 wavelengths long?
Expand Hint
For any normal distribution, the table for the unit normal distribution can be utilized via the following transformation:
$$$z=\frac{x-\mu }{\sigma }$$$
where
$$z$$
is the “Z” score associated with the unit normal distribution table,
$$\mu$$
is the mean,
$$\sigma$$
is the standard deviation, and
$$x$$
is the desired region under the bell curve.
Hint 2
$$$z=\frac{x-\mu }{\sigma }=\frac{6-5}{1.25}=0.8$$$
For any normal distribution, the table for the unit normal distribution can be utilized via the following transformation:
$$$z=\frac{x-\mu }{\sigma }$$$
where
$$z$$
is the “Z” score associated with the unit normal distribution table,
$$\mu$$
is the mean,
$$\sigma$$
is the standard deviation, and
$$x$$
is the desired region under the bell curve.
$$$z=\frac{x-\mu }{\sigma }=\frac{6-5}{1.25}=0.8$$$
Referring to the Unit Normal Distribution Table like the one in the FE Handbook:
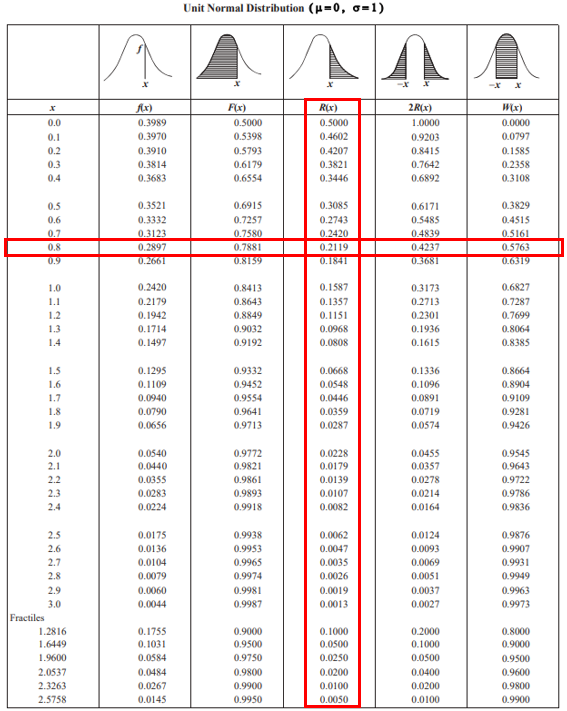
The left most column contains all the possible values for Z. The red horizontal highlight refers to the the problem’s calculated Z score of 0.8. Because the problem statement asks to include all signals longer than 6 wavelengths on the distribution, the
$$R(x)$$
column is also highlighted in red. The intersecting value of these two row/column is 0.2119, which is the probability of a signal with more than 6 wavelengths being randomly selected.
0.2119
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Normal Distribution (Gaussian Distribution)
114. Obstacle Course
621. Z Score
Similar Problems from FE Section: Probability Functions, Distributions, and Expected Values
114. Obstacle Course
621. Z Score